Inequalities - Representation on the Number Line
The numbers, which satisfy an inequality can be illustrated on a number line. For instance we may need to illustrate all the number that satisfy the inequality: \[x < 5 \] in other words we have to show all the numbers that make the inequality true.
To illustrate these numbers we'll often use a number line. For the inequality \(x < 5 \) this is shown here:
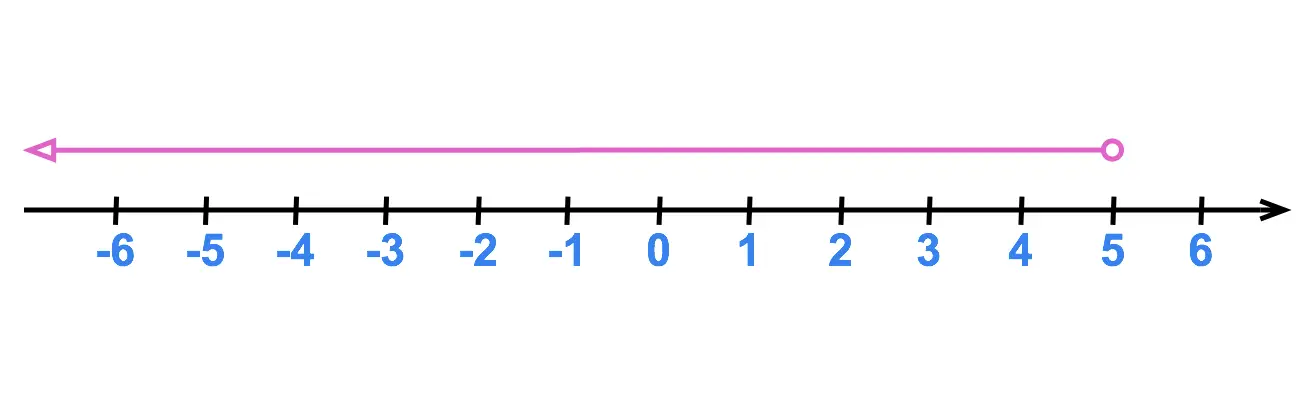
The following tutorial will teach us all we need to know about inequalities and number lines for now.
Summary - Inequalities & Number Line
Following the tutorial we've just seen, below we list how to illustrate the four types of inequalities on the number line.
Greater Than: \(x > a\)
\(x > a \) is represented by an arrow with an empty dot above the \(a\).The arrow points in the direction of all the numbers that are greater than \(a\).
The empty dot highlights that fact that \(x\) cannot equal \(a\):

Greater Than Or Equal To: \(x \geq a\)
\(x \geq a \) is represented by an arrow with an filled-in dot above the \(a\).The arrow points in the direction of all the numbers that are greater than \(a\).
The filled-in dot highlights that fact that \(x\) can be equal to \(a\):

Less Than: \(x < a\)
\(x < a \) is represented by an arrow with an empty dot above the \(a\).The arrow points in the direction of all the numbers that are less than \(a\).
The empty dot highlights that fact that \(x\) cannot equal \(a\):

Less Than Or Equal To: \(x \leq a\)
\(x \leq a \) is represented by an arrow with an filled-in dot above the \(a\).The arrow points in the direction of all the numbers that are less than \(a\).
The filled-in dot highlights that fact that \(x\) can be equal to \(a\):

Exercise
Illustrate the solutions to each of the following inequalities using the number line:
- \(x \leq 4 \)
- \(x > -3 \)
- \(x < 6 \)
- \(x \geq 1\)
- \(x \leq -1 \)
- \(x > 2 \)
Answers Without Working
-
The solutions to \(x \leq 4 \) are all numbers less than or equal to \(4\):

-
The solutions to \(x > -3 \) are all numbers greater than \(-3\):

-
The solutions to \(x < 6 \) are all numbers less than \(6\):

-
The solutions to \(x \geq 1 \) are all numbers greater than or equal to \(1\):

-
The solutions to \(x \leq -1 \) are all numbers less than or equal to \(-1\):

-
The solutions to \(x > 2 \) are all numbers greater than \(2\):

Scan this QR-Code with your phone/tablet and view this page on your preferred device.

 Subscribe to Our Channel
Subscribe to Our Channel
Subscribe Now and view all of our playlists & tutorials.