Cubic Sequences
(Difference Method for the \(n^{\text{th}}\) term)
Cubic sequences are characterized by the fact that the third difference between its terms is constant.
For example, consider the sequence:
\[4,14,40,88,164, \dots \]
looking at the first, second and third difference of this sequence would look like:
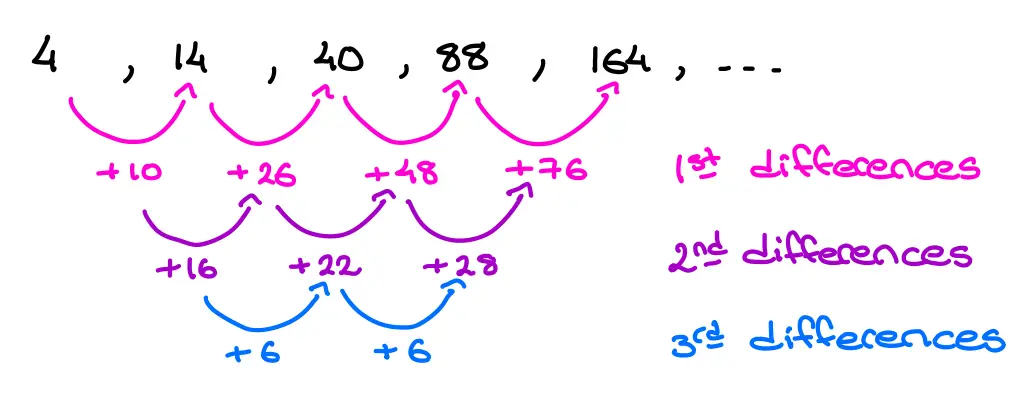
Looking at this we can see that the third difference is constant, and not equal to zero, this means it is a cubic sequence.
Formula for the \(n^{\text{th}}\) term
If a sequence is cubic then its formula can be written:
\[u_n = an^3+bn^2+cn + d\]
For example, the sequence, we saw above: \(4,14,40,88,164, \dots \) has formula:
\[u_n = n^3 + 2n^2 - 3n + 4 \]
Indeed, if we replace \(n\) by (for example) \(1\) and \(2\) we'll find the first and second terms of the sequence, that's:
\[\begin{aligned} u_1 & = 1^3 + 2\times 1^2 - 3 \times 1 + 4 \\
&= 1 + 2 - 3 + 4 \\
u_1 & = 4 \end{aligned} \]
and
\[\begin{aligned} u_2 &= 2^3 + 2\times 2^2 - 3 \times 2 + 4 \\
& = 8 + 2\times 4 - 6 + 4 \\
& = 8+8-6+4 \\
u_2 & = 14 \end{aligned} \]
We learn
how to find the formula for the \(n^{\text{th}}\) term below.
Method - Finding the formula for the \(n^{\text{th}}\) term
Given the first few terms of a cubic sequence, we find its formula
\[u_n = an^3+bn^2+cn +d\]
using the following four equations:
\[\begin{cases}
6a = \text{third difference} \\
12a + 2b = \text{1st second difference} \\
7a + 3b + c = \text{difference between the first two terms} \\
a + b + c + d = \text{first term}
\end{cases}\]
This provides us with four equations, which we solve from top to bottom, to find each of the four unknown coefficients \(a\), \(b\), \(c\) and \(d\).
The four equations, stated above, can be a little confusing so we illustrate it here here with an example.
Consider the sequence whose first few terms are:
\[4,14,40,88,164, \dots \]
The following illustration shows where each of the four equations, stated above, fits in.:
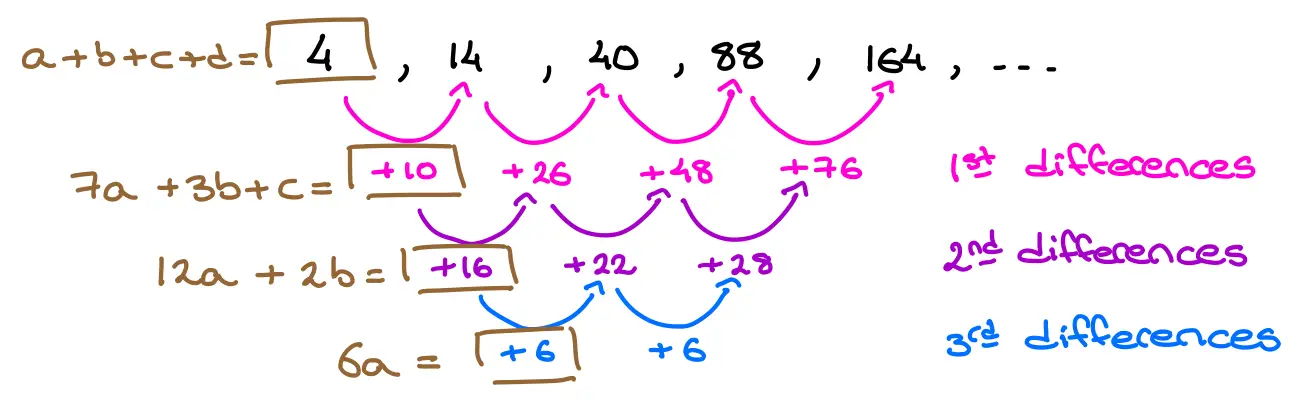
We can see that the values that we use, the ones we've boxed in the illustration, are always the first on each row.
We therefore have four equations to solve:
\[\begin{cases}
6a = 6 \\
12a + 2b = 16 \\
7a + 3b + c = 10 \\
a + b + c + d = 4
\end{cases}\]
We solve these working from top to bottom. Each time we move-on to solve a new equation we substitute the value we just found in the previous equations:
-
equation 1:
We start with the first (top) equation:
\[\begin{aligned}
& 6a = 6 \\
& a = \frac{6}{6} \\
& a = 1
\end{aligned}\]
Now that we know the value of \(a\), \(a =1\), we move-on to the second equation.
-
equation 2:
We have to solve \(12a + 2b = 16\). Now that we know that \(a=1\) this becomes:
\[\begin{aligned}
& 12\times 1 + 2b = 16 \\
& 12 + 2b = 16 \\
& 2b = 16 - 12 \\
& 2b = 4 \\
& b = \frac{4}{2} \\
& b = 2
\end{aligned}\]
Now that we know the value of \(b\), \(b =2\), we move-on to the third equation.
-
equation 3:
We have to solve \(7a + 3b + c = 10\). Since we know that \(a=1\) and \(b = 2\) this becomes:
\[\begin{aligned}
& 7 \times 1 + 3 \times 2 + c = 10 \\
& 7 + 6 + c = 10 \\
& 13 + c = 10 \\
& c = 10 - 13 \\
& c = -3
\end{aligned}\]
Now that we know the value of \(c\), \(c = -3\), we move-on to the fourth equation.
-
equation 4:
We have to solve \(a + b + c + d = 4\). Since we know that \(a=1\), \(b = 2\) and \(c = -3\) this becomes:
\[\begin{aligned}
& 1 + 2 - 3 + d = 4 \\
& 3 - 3 + d= 4 \\
& d = 4
\end{aligned}\]
Now that we know the value of \(d\), \(c = 4\), we can finally state the formula for the n-th term of this cubic sequence:
\[u_n = n^3 + 2n^2 - 3n + 4\]
Exercise
Find the formula for the \(n^{\text{th}}\) term of each of the following sequences:
-
The sequence whose first few terms are:
\[4,14,40,88,164, \dots \]
-
The sequence whose first few terms are:
\[4,23,66,145,272, \dots \]
-
The sequence whose first few terms are:
\[-1,1,-5,-25,-65, \dots \]
-
The sequence whose first few terms are:
\[1,14,65,178,377, \dots \]
-
The sequence whose first few terms are:
\[11,6,-25,-100,-237, \dots \]
Note: this exercise can be downloaded as a worksheet to practice with:
worksheet


