Tangents & Normals
(equation of the tangent and the normal to the curve at point \(P\))
In this section we learn how to find the equation of the tangent and the normal to a curve at a point along its length.
For each we learn a two-step method as well as view a tutorial and work our way through exercises to consolidate our knowlede.

Tangent to a Curve
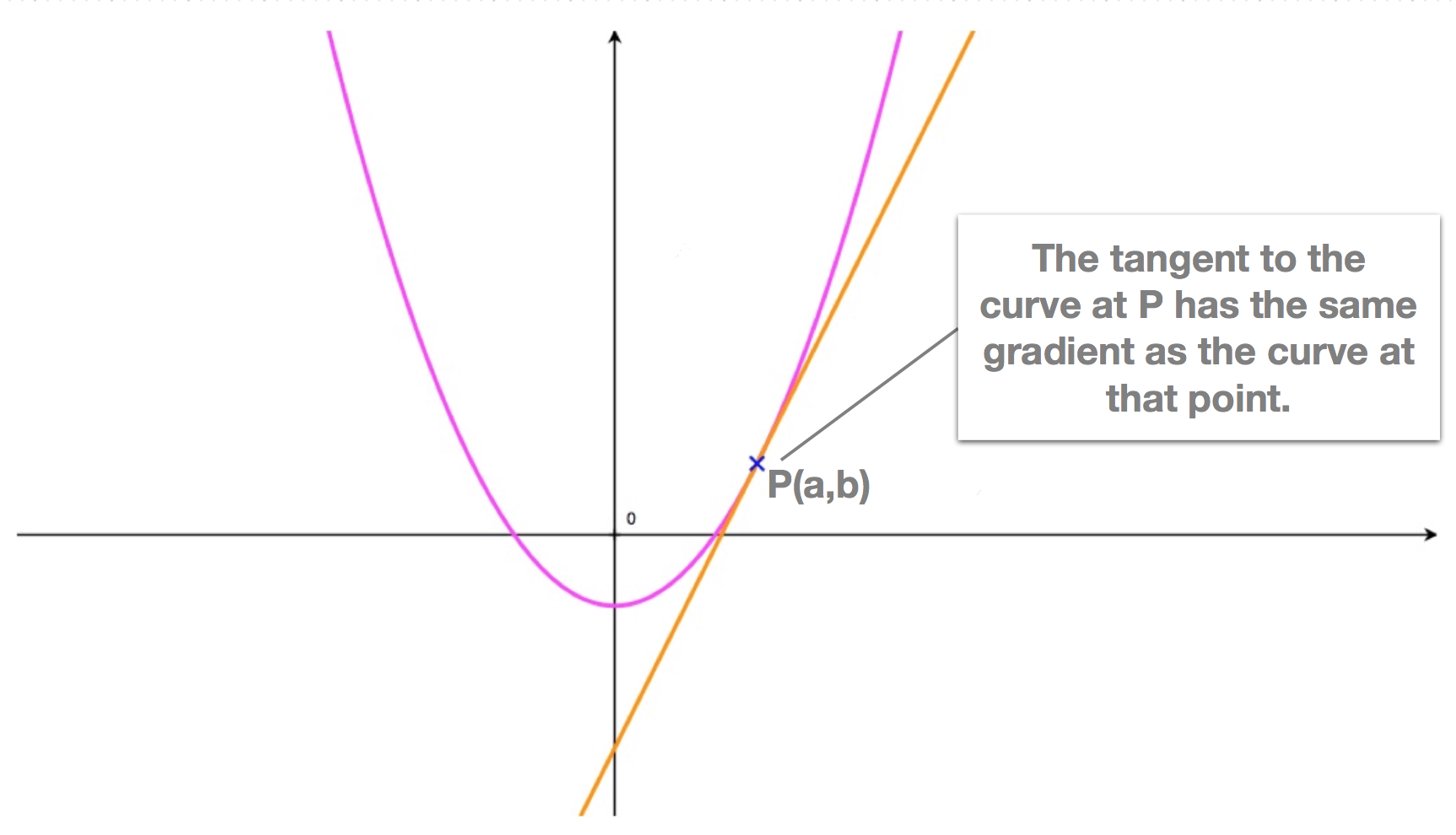
The tangent to a curve at a point \(P\) along its length is the line which passes through point \(P\) and has same gradient as the curve at \(P\).Say the curve has equation \(y = f(x)\), then its gradient at a point \(P\begin{pmatrix}a,b\end{pmatrix}\) along its length is equal to: \[f'(a)\] Where \(f'(a)\) is the derivative of \(f(x)\) evaluated at \(x = a\).
So the tangent will have gradient: \[m = f'(a)\]
Illustration - Tangent
Normal to a Curve
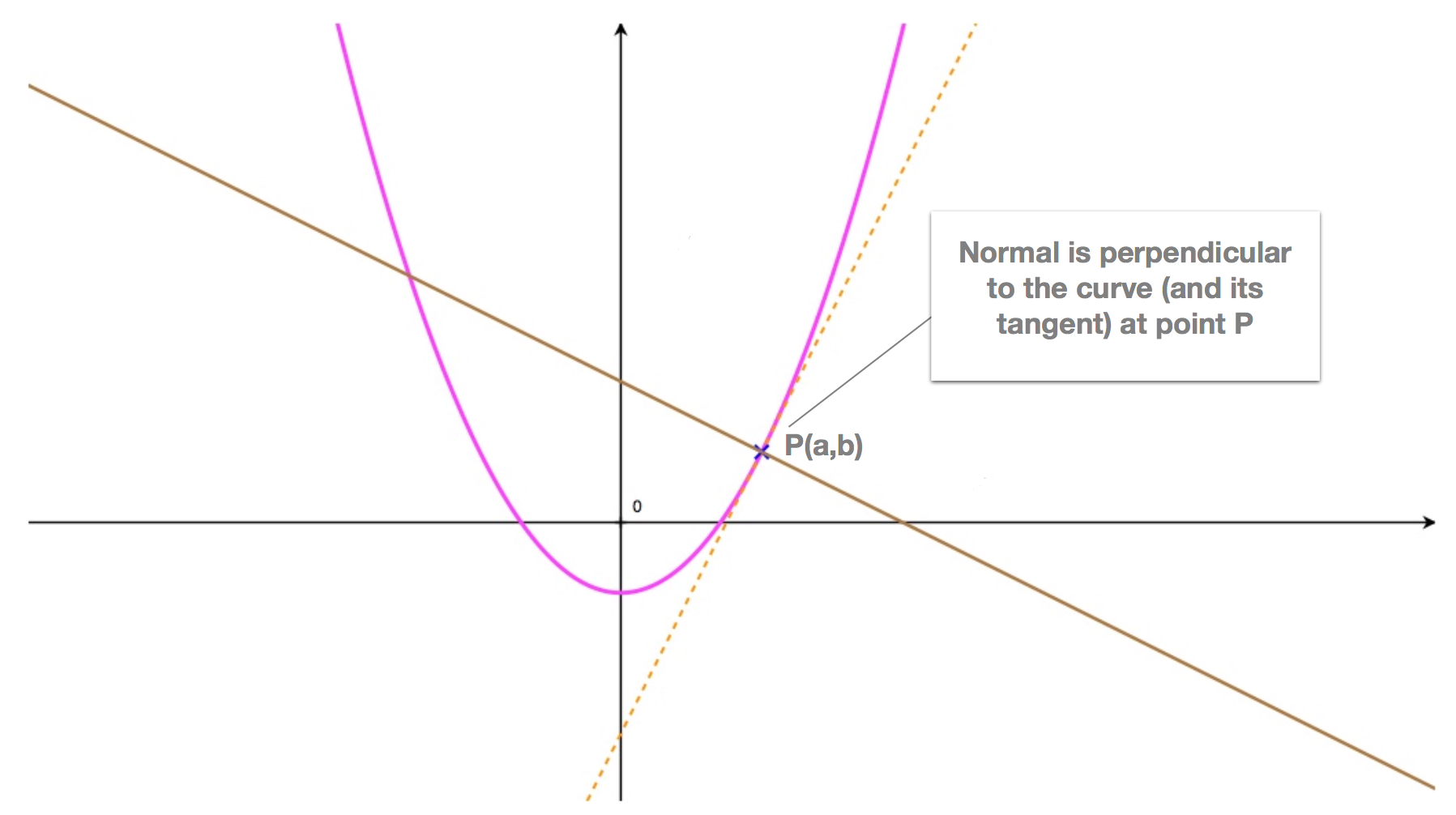
The normal to a curve at a point \(P\) along its length is the line which passes through point \(P\) and is perpendicular to the tangent at \(P\).
Say the curve has equation \(y = f(x)\), then its gradient at a point \(P\begin{pmatrix}a,b\end{pmatrix}\) along its length is equal to: \[f'(a)\] Since the normal is perpendicular to the tangent, its gradient is the negative reciprocal of the gradient of the tangent. That's: \[m = -\frac{1}{f'(a)}\]
Illustration - Normal
How to find the Equation of a Tangent & a Normal
A tangent to a curve as well as a normal to a curve are both lines. They therefore have an equation of the form: \[y = mx+c\] The methods we learn here therefore consist of finding the tangent's (or normal's) gradient and then finding the value of the \(y\)-intercept \(c\) (like for any line).
We start by learning how to find the equation of a tangent to a curve. Further-down, we learn how to find the equation of a normal.
Method: Equation of the Tangent to a Curve
Given a function \(f(x)\), described by a curve \(y=f(x)\), we find the equation of the tangent to the curve at a point \(P\begin{pmatrix}a,b\end{pmatrix}\) along its length, in two steps:
-
Step 1: find the gradient of the curve at point \(P\begin{pmatrix}a,b\end{pmatrix}\), this equals to the gradient of the tangent
.
The gradient of the curve at \(P\begin{pmatrix}a,b\end{pmatrix}\) equals to the derivative, \(f'(x)\), evaluated at \(x = a\): \[f'(a)\] By definition, the tangent's gradient \(m\) at \(P\) equals to the curve's gradient at \(P\begin{pmatrix}a,b\end{pmatrix}\), so: \[m = f'(a)\] - Step 2: find the tangent's equation in the form \(y=mx+c\) by making \(y\) the subject in the formula: \[y-b = m \begin{pmatrix}x - a \end{pmatrix}\] where \(a\) and \(b\) are the \(x\) and \(y\) coordinates of point \(P\) and \(m\) is the gradient of the curve at point \(P\) (found in step 1).
Tutorial
In the following tutorial we illustrate how to use this two-step method with two examples, in which we find:
- the tangent to the curve of the function \(f(x) = x^2 - 1\) at the point \(P\begin{pmatrix}2,3\end{pmatrix}\).
- the tangent to the curve of the function \(f(x) = x^2 - 1\) at the point \(P\begin{pmatrix}2,3\end{pmatrix}\).
Example
Find the equation of the tangent to the curve \[y = x^2 - 4\] at the point along its length with coordinates \(\begin{pmatrix}3,5\end{pmatrix}\).
Exercise 1
-
Given the function defined by:
\[f(x) = 2x^2 - 2\]
- Find \(f'(x)\).
- Calculate \(f'(2)\).
- Find the equation of the tangent to this function's graph \(y=2x^2-2\) at the point along its length with coordinates \(\begin{pmatrix}2,6 \end{pmatrix}\)
-
Consider the function defined by:
\[f(x) = 5x+\frac{3}{x}\]
- Calculate the \(y\)-coordinate of the curve \(y=f(x)\) when \(x = 1\). State the coordinates of the point on the curve with \(x\)-coordinate \(x = 1\).
- Find an expression for \(f'(x)\).
- Find the equation of the tangent to the curve \(y=f(x)\) at the point along its length with \(x\)-coordinate \(x = 1\).
Answers Without Working
-
Given the function defined by:
\[f(x) = 2x^2 - 2\]
- For \(f'(x)\), we find: \[f'(x) = 4x\]
- We find: \[f'(2)= 8\]
- We find the equation of the tangent to be: \[y=8x-10\]
-
- The \(y\)-coordinate when \(x=1\) is \(f(1)\). We find: \[y = 8\] So the point along the curve with \(x\)-coordinate \(x = 1\) is: \[\begin{pmatrix}1,8\end{pmatrix}\]
- We find: \[f'(x) = 5 - \frac{3}{x^2}\]
- The tangent to the curve at the point \(\begin{pmatrix}1,8\end{pmatrix}\) has equation: \[ y = 2x+6\]
Method: Equation of the Normal to a Curve
Given a function \(f(x)\), described by a curve \(y=f(x)\), we find the equation of the normal to the curve at a point \(P\begin{pmatrix}a,b\end{pmatrix}\) along its length, in three steps:
-
Step 1: find the gradient of the curve at point \(P\begin{pmatrix}a,b\end{pmatrix}\).
By definition this equals to the derivative, \(f'(x)\), evaluated at \(x = a\): \[f'(a)\] -
Step 2: find the gradient of the normal to the curve at \(P\begin{pmatrix}a,b\end{pmatrix}\).
The normal's gradient \(m\) is the negative reciprocal of the gradient of the curve at the point \(P\begin{pmatrix}a,b\end{pmatrix}\), that's: \[m = -\frac{1}{f'(a)}\] - Step 3: find the normal's equation in the form \(y=mx+c\) by making \(y\) the subject in the formula: \[y-b = m \begin{pmatrix}x - a \end{pmatrix}\] where \(a\) and \(b\) are the \(x\) and \(y\) coordinates of point \(P\) and \(m\) is the gradient of the curve at point \(P\) (found in step 2).
Example
Find the equation of the normal to the curve \[y = \frac{x^2}{2}-\frac{5}{2}\] at the point along its length with coordinates \(\begin{pmatrix}3,2\end{pmatrix}\).
Exercise 2
-
Given the function defined by:
\[f(x)= x^2-1\]
- Find the \(y\)-coordinate of the point along the curve \(y=f(x)\), with \(x\)-coordinate \(x = 2\). Call this point \(P\).
- Find an expression for \(f'(x)\).
- Find the gradient of the curve \(y=f(x)\) at point \(P\).
- State the value of the gradient of the normal to the curve \(y=f(x)\) at point \(P\).
- Find the equation of the normal to the curve \(y=f(x)\) at point \(P\).
-
Given the function defined as:
\[y = 4x + \frac{9}{x}\]
- Calculate the \(y\)-coordinate of the point along the function's curve with \(x\)-coordinate \(x = 3\). Call this point \(P\).
- Find \(\frac{dy}{dx}\).
- Find the gradient of the curve \(y = 4x + \frac{9}{x}\) at point \(P\).
- State the value of the gradient of the normal to the curve at point \(P\).
- Find the equation of the normal to the curve at point \(P\).
Answers Without Working
-
- The \(y\) coordinate is equal to \(f(2)\). We find: \[y = 3\] So \(P\) has coordinates: \[P\begin{pmatrix}2,3\end{pmatrix}\]
- We find: \[f'(x)=2x\]
- The gradient of the curve at \(P\) equals to \(f'(2)\). We find: \[f'(2)=4\]
- The normal to the curve at \(P\) has a gradient equal to the negative reciprocal of the gradient of the curve at \(P\). That's: \[m = - \frac{1}{4}\]
- The equation of the normal to the curve at point \(P\) is: \[y = - \frac{x}{4}+\frac{7}{2}\]
-
- When \(x=3\), we find \(y=15\). So point \(P\) has coordinates: \[P\begin{pmatrix}3,15\end{pmatrix}\]
- We find: \[\frac{dy}{dx} = 4 - \frac{9}{x^2}\]
- The gradient of the curve \(y = 4x + \frac{9}{x}\) at point \(P\) equals to the derivative \(\frac{dy}{dx}\) when \(x = 3\). We find: \[\frac{dy}{dx} = 3\]
- The gradient \(m\) of the normal to the curve at point \(P\) is the negative reciprocal of the gradient of the curve at \(P\), that's: \[m = -\frac{1}{3}\]
- The equation of the normal to the curve at point \(P\) is: \[y = - \frac{x}{3}+16\]