Defining the Cosine and Sine Functions on the Unit Circle
(\(sin(x)\) & \(cos(x)\))
The cosine and sine functions: \[cos(x) \quad \text{and} \quad \ sin(x)\] both have definitions linked to the coordinates of a point \(P\), which is on the circumference of a unit circle.
Unit Circle
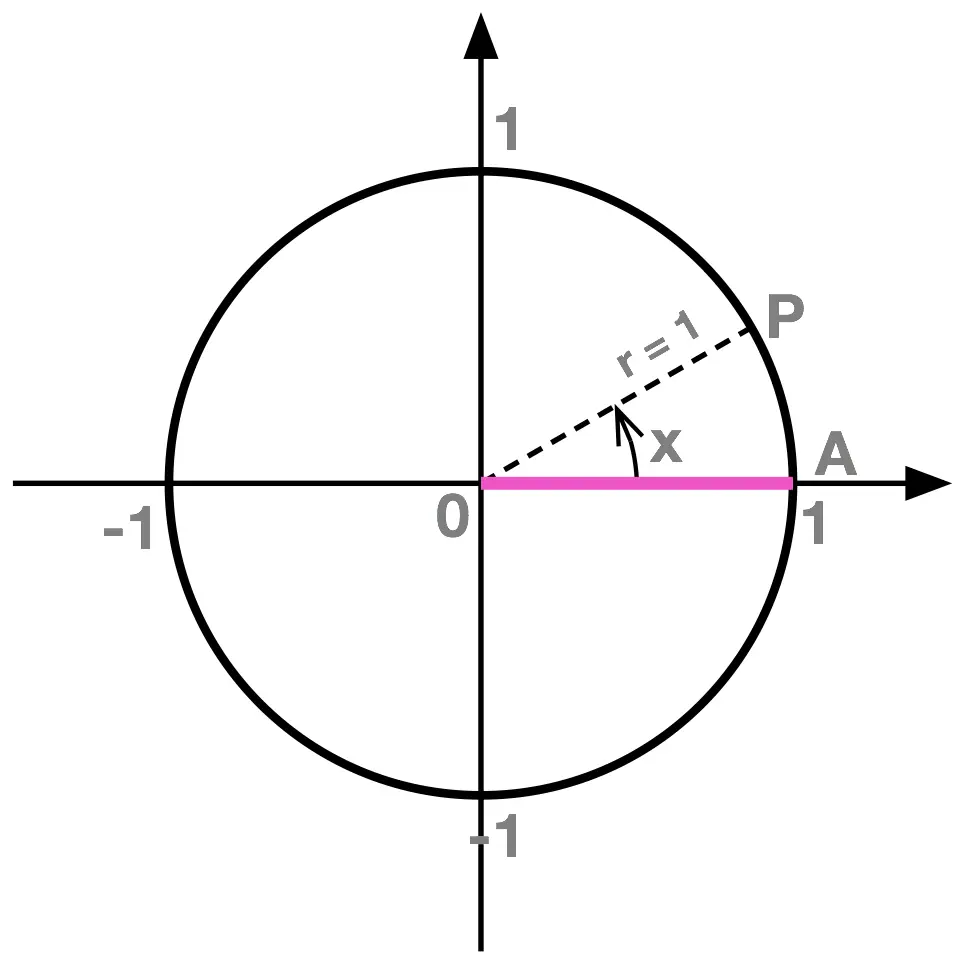 A unit circle is centered at the origin of a Cartesian Plane and has unit radius, \(r=1\).
A unit circle is centered at the origin of a Cartesian Plane and has unit radius, \(r=1\).
When working with the functions \(cos(x)\) and \(sin(x)\) the variable \(x\) is:
the angle, measured anti-clockwise, from the radius \(OA\) to the radius \(OP\).
Note: an angle measured clockwise is negative.
Definition: \(cos(x)\) and \(sin(x)\)
Given a unit circle, centered at the origin with a point \(P\) on its circumference, \(cos(x)\) and \(sin(x)\) are defined as follows:
- \(cos(x)\) is the horizontal coordinate of the point.
- \(sin(x)\) is the vertical coordinate of the point.
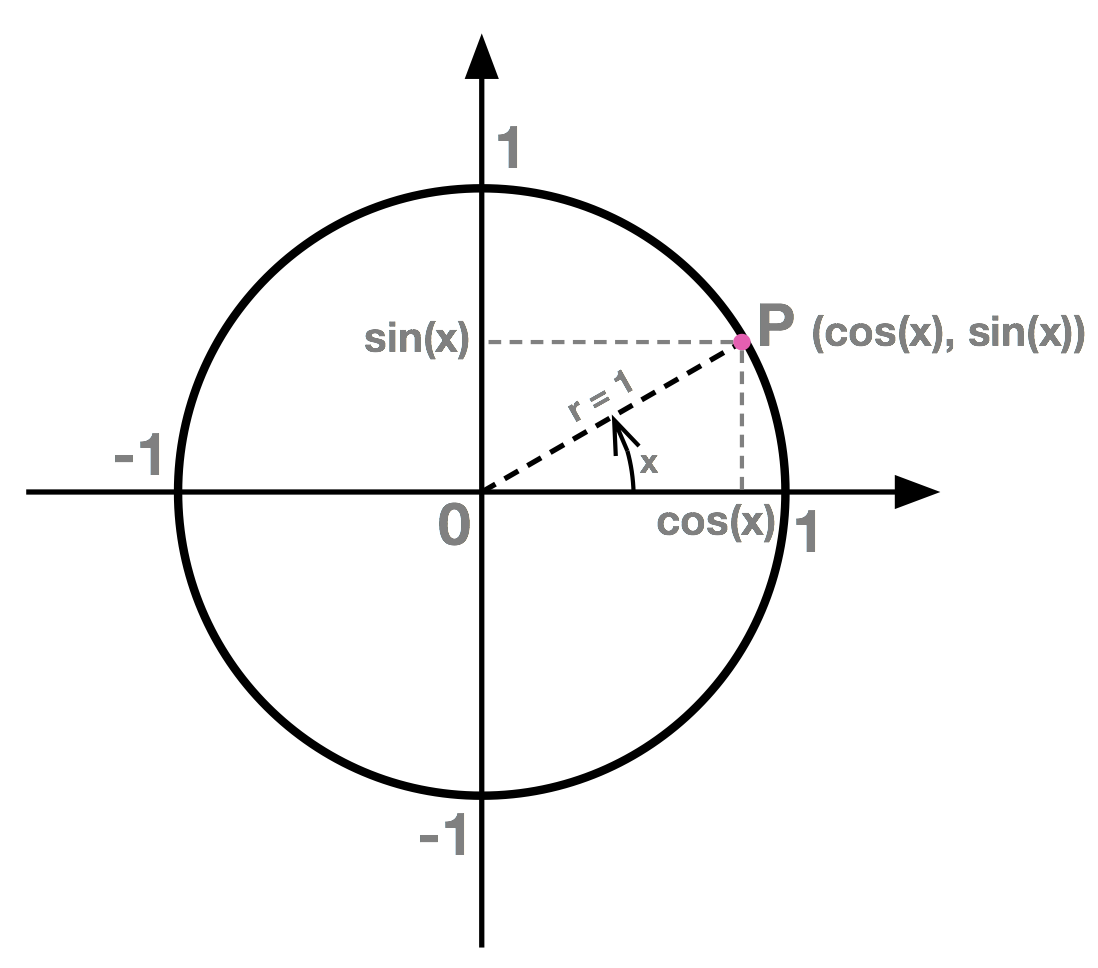 Each of these two definitions are illustrated in the unit circle shown here.
Each of these two definitions are illustrated in the unit circle shown here.
-
The function \(cos(x)\) has input value the angle \(x\) and output value the horizontal coordinate of point \(P\) as it moves around the unit circle.
- The function \(sin(x)\), on the other hand, has input value the angle \(x\) and output value the vertical coordinate of point \(P\).
Tutorial: definition of \(cos(x)\) & \(sin(x)\)
In the following tutorial we learn and illustrate what the \(cos(x)\) and \(sin(x)\) fucntions are and how we can find the value of either of them, for a given \(x\), using the unit circle.
Domain and Range of \(cos(x)\) & \(sin(x)\)
Domain
Both \(cos(x)\) and \(sin(x)\) are defined for all real numbers.
Indeed no matter what angle \(x\) is, the two functions are perfectly well-defined.
Note: if \(x>360^{\circ}\) or \(x<360^{\circ}\) then the point \(P\) will have done more than one full turn around the unit circle.
Unless otherwise told, the domain of both \(cos(x)\) and \(sin(x)\) is:
\[\text{Domain} = \mathbb{R}\]
Range
Since point \(P\) is "stuck" on the circumference of a unit cirlce, centered at the origin: its coordinates will never be less than \(-1\), nor greater than \(1\).
Consequently, the following result will always be true:
\[-1\leq cos(x) \leq 1\]
\(cos(x)\) & \(sin(x)\) are Periodic Functions
Both \(cos(x)\) and \(sin(x)\) are periodic functions.
This means that their output values repeat themselves at regular intervals.
The interval after which they repeat themselves is known as the period and is usually referred to with the letter \(T\).
Period of \(sin(x)\) & \(cos(x)\)
Both \(sin(x)\) and \(cos(x)\) are periodic with period: \[T = 360^{\circ}\] Consequently the following two results will always be true: \[cos\begin{pmatrix}x+360k \end{pmatrix} = cos(x), \quad k \in \mathbb{Z}\]
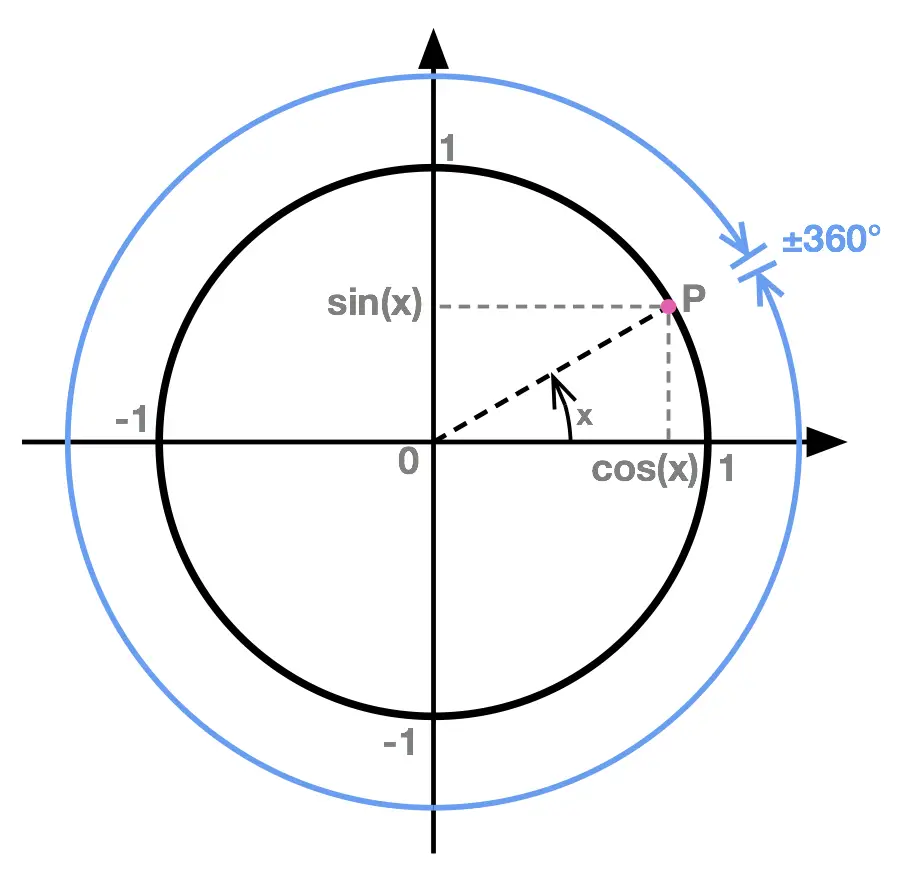 The fact that the values of \(cos(x)\) and \(sin(x)\) don't change when we add, or subtract, \(360\) to \(x\) is illustrated here.
The fact that the values of \(cos(x)\) and \(sin(x)\) don't change when we add, or subtract, \(360\) to \(x\) is illustrated here.
No matter where \(P\) is on the circumference of the circle, if we add (or subtract) \(360^{\circ}\) to the angle \(x\) we'll do a full turn of the unit circle and be at the same point of its circumference.
This will also be true if we add (or subtract) \(720^{\circ} = 360^{\circ}\times 2\), \(1080^{\circ} = 360^{\circ} \times 3\), ... or any multiple or \(360^{\circ}\); since in each case we'll still end-up at the same point \(P\) on the circle.
This explains the result, we saw further-up:
\[cos\begin{pmatrix}x+360k \end{pmatrix} = cos(x), \quad k \in \mathbb{Z}\]
Tutorial: \(cos(x)\) & \(sin(x)\) Periodic Functions
Well-known \(sin(x)\) and \(cos(x)\) values
Some values of \(cos(x)\) and \(sin(x)\) are considered as "well-known" and must be known off-by-heart when studying trigonometry and the sine and cosine functions.
These are the values of both \(sin(x)\) and \(cos(x)\) for the angles \(0^{\circ}\), \(30^{\circ}\), \(45^{\circ}\), \(60^{\circ}\) and \(90^{\circ}\).
The values are shown in the following table:
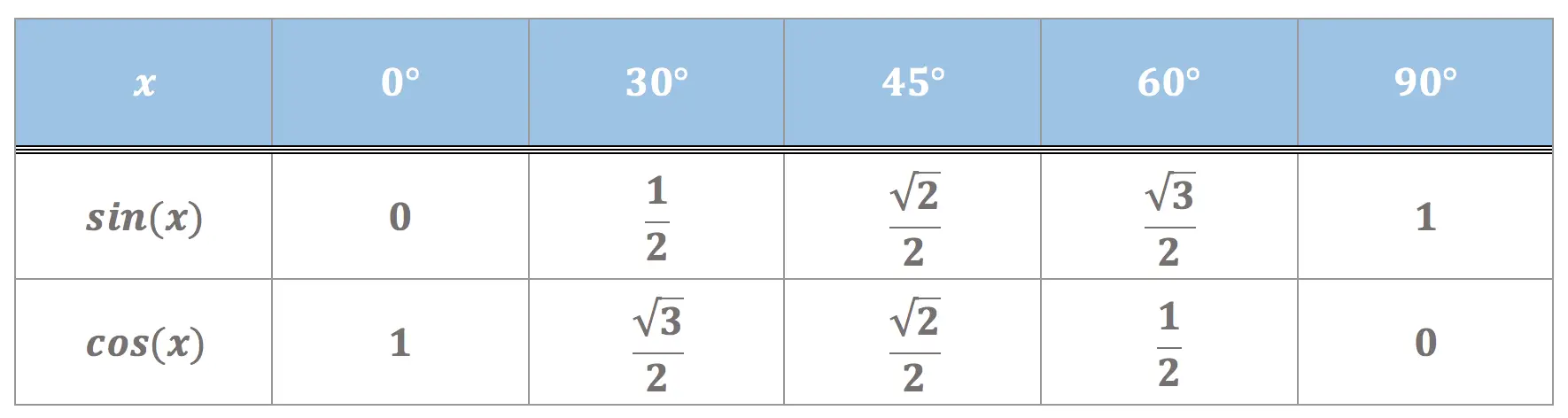
These are the values of both \(sin(x)\) and \(cos(x)\) for the angles \(0^{\circ}\), \(30^{\circ}\), \(45^{\circ}\), \(60^{\circ}\) and \(90^{\circ}\).
Working in all quadrants with the unit circle
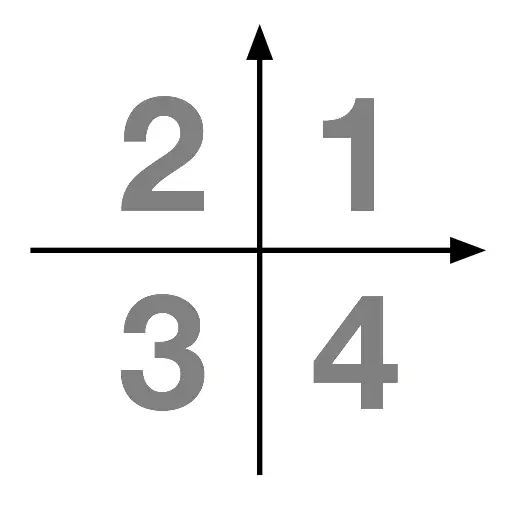 All of the well-known angles are in the quadrant 1 of the Cartesian grid.
All of the well-known angles are in the quadrant 1 of the Cartesian grid.
Using the symmetry of the circle we can extrapolate the equivalent well-known angles in each of the other three quadrants, \(2\), \(3\) and \(4\).
- in quadrant 2: a point in on the unit circle in quadrant \(2\) can be brought back to (compared to) quadrant 1 by reflecting it across the vertical axis.
- in quadrant 3: a point on the unit circle in quadrant \(3\) can be brought back to (compared to) quadrant 1 by looking at the point diametrically opposite it on the unit circle.
- in quadrant 4: a point in on the unit circle in quadrant \(4\) can be brought back to (compared to) quadrant 1 by reflecting it across the horizontal axis.
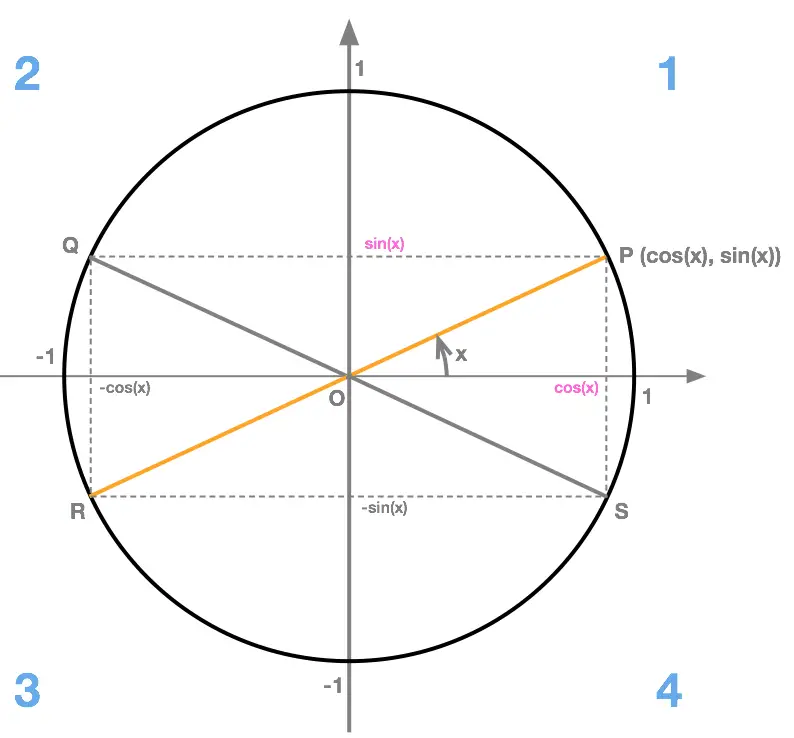
Illustration
Consider a unit circle, with a point \(P\) on its circumference, which is in Quadrant 1 whose coordinates are \(P\begin{pmatrix}cos(x),sin(x)\end{pmatrix}\).
- Point \(Q\) is in quadrant 2. We can deduce its coordinates from the fact that it is the reflection of point \(P\) across the vertical axis: \[Q\begin{pmatrix}-cos(x),sin(x)\end{pmatrix}\]
- Point \(R\) is in quadrant 3. We can deduce its coordinates from the fact that it is diametrically opposite point \(P\): \[R\begin{pmatrix}-cos(x),-sin(x)\end{pmatrix}\]
- Point \(S\) is in quadrant 4. We can deduce its coordinates from the fact that it is the reflection of point \(P\) across the horizontal axis: \[S\begin{pmatrix}cos(x),-sin(x)\end{pmatrix}\]
Tutorial: \(cos(x)\) and \(sin(x)\) in the Second Quadrant
In the following tutorial we learn and illustrate how to use the unit circle to find the values of both \(cos(x)\) and \(sin(x)\) when \(90^{\circ} < x < 180^{\circ}\) or \(-270^{\circ} < x < -180^{\circ} \); in other words when the point on the unit circle is in the second quadrant.
We work through three examples, in which we show how to find:
- \(cos(150)\) and \(sin(150)\)
- \(cos(120)\) and \(sin(120)\)
- \(cos(-225)\) and \(sin(-225)\)
The method we've just learned can be summarized with a five-step method, we've written it here:
Method: angles in the second quadrant
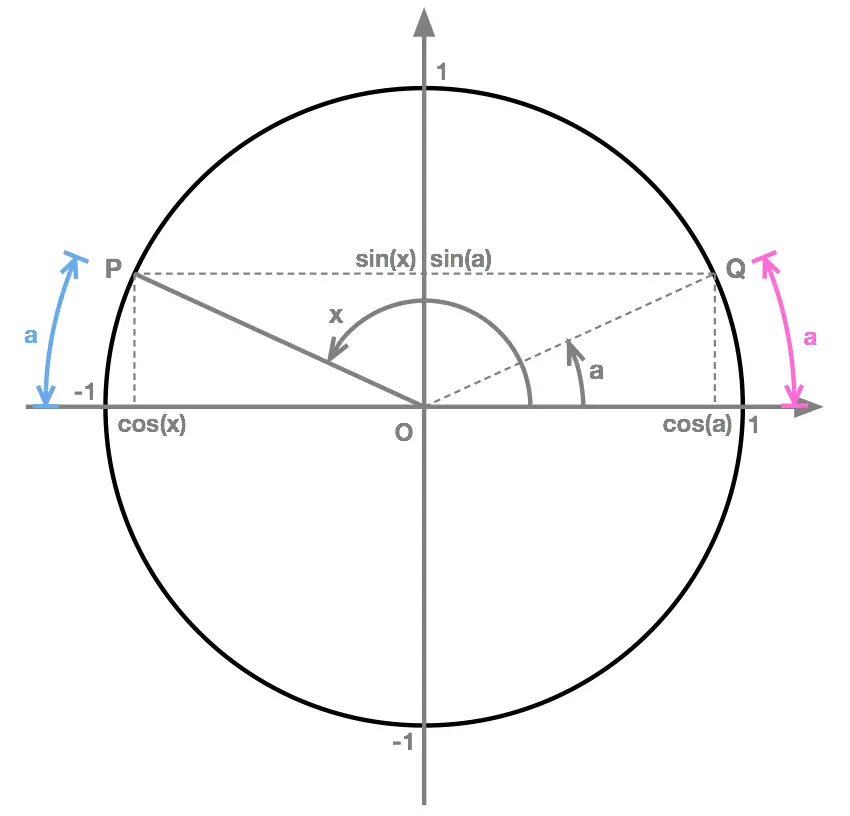 When the angle \(x\) is such that point \(P\), on the unit circle, lies in the second quadrant we can find the value of \(cos(x)\) and \(sin(x)\) following the steps:
When the angle \(x\) is such that point \(P\), on the unit circle, lies in the second quadrant we can find the value of \(cos(x)\) and \(sin(x)\) following the steps:
- Step 1: measure the angle \(a\) separating \(P\) from \(180^{\circ}\).
- Step 2: reflect \(P\) across the vertical axis to define the "new" point \(Q\) on the unit circle.
- Step 3: notice that \(Q\) is at an angle \(a \) from the angle \(0^{\circ}\) (the "starting point").
- Step 4: find the cordinates of point \(Q\), using the fact that \(Q\) has coordinates: \[Q\begin{pmatrix}cos(a ), sin(a ) \end{pmatrix}\]
-
Step 5: find the coordinates of point \(P\):
\[P\begin{pmatrix}cos(x), sin(x) \end{pmatrix}\]
using the fact that:
\[cos(x) = - cos(a)\]
and \[sin(x) = sin(a)\]
Exercise
Without a calculator, find each of the following:
- \(sin(120)\)
- \(cos(120)\)
- \(sin(-210)\)
- \(cos(-210)\)
- \(sin(135)\)
- \(cos(135)\)
- \(sin(150)\)
- \(cos(150)\)
Tutorial: Working in Quadrant 3
In the following tutorial we learn and illustrate how to use the unit circle to find the values of both \(cos(x)\) and \(sin(x)\) when \(180^{\circ} < x < 270^{\circ}\) or \(-180^{\circ} < x < -90^{\circ} \); in other words when the point on the unit circle is in the third quadrant.
We work through three examples, in which we show how to find:
- \(cos(210)\) and \(sin(210)\)
- \(cos(225)\) and \(sin(225)\)
- \(cos(-120)\) and \(sin(-120)\)
Method: angles in the third quadrant
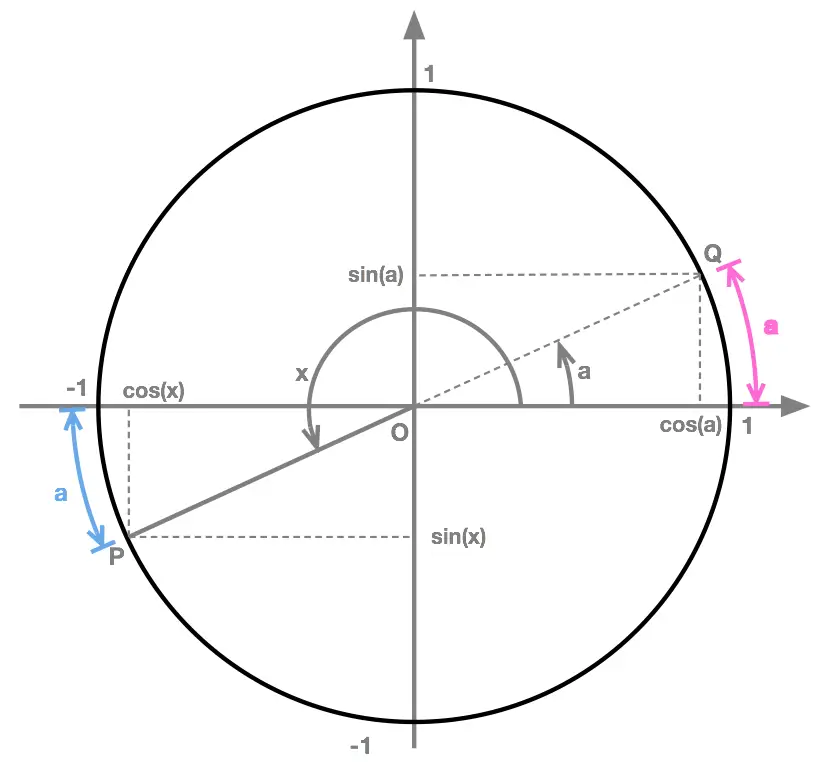 When the angle \(x\) is such that point \(P\), on the unit circle, lies in the third quadrant we can find the value of \(cos(x)\) and \(sin(x)\) following the steps:
When the angle \(x\) is such that point \(P\), on the unit circle, lies in the third quadrant we can find the value of \(cos(x)\) and \(sin(x)\) following the steps:
- Step 1: measure the angle \(a\) separating \(P\) from \(180^{\circ}\).
- Step 2: define the "new" point \(Q\) diametrically opposite point \(P\) on the unit circle.
- Step 3: notice that \(Q\) is at an angle \(a \) from the angle \(0^{\circ}\) (the "starting point").
- Step 4: find the cordinates of point \(Q\), using the fact that \(Q\) has coordinates: \[Q\begin{pmatrix}cos(a ), sin(a ) \end{pmatrix}\]
-
Step 5: find the coordinates of point \(P\):
\[P\begin{pmatrix}cos(x), sin(x) \end{pmatrix}\]
using the fact that:
\[cos(x) = - cos(a)\]
and \[sin(x) = -sin(a)\]
Tutorial: Working in Quadrant 4
In the following tutorial we learn how to find \(cos(x)\) and \(sin(x)\) when \(270^{\circ} < x < 360^{\circ} \), or \(-90^{\circ} < x < 0^{\circ} \).
We work through three examples, in which we show how to find:
- \(cos(330)\) and \(sin(330)\)
- \(cos(-45)\) and \(sin(-45)\)
- \(cos(300)\) and \(sin(300)\)
Exercise 1
Answer each of the following questions:
- What is the domain of \(cos(x)\)?
- What is the domain of \(sin(x)\)?
- What is the range of \(cos(x)\)?
- What is the range of \(sin(x)\)?
- What is the period of \(cos(x)\) and \(sin(x)\)?
-
Answer "true" or "false" to each of the following statements:
- \(sin(x+360) = sin(x)\)
- \(cos(x+180) = -cos(x)\)
- \(cos(x-360) = -cos(x)\)
- \(sin(-x) = sin(x)\)
- \(cos(-x) = cos(x)\)
- \(sin(30) = sin(150) = -sin(210) = -sin(330)\)
- \(cos(45) = cos(315)\)
Answers Without Working
- The domain of \(cos(x)\) is all real numbers \(\mathbb{R}\).
- The domain of \(sin(x)\) is all real numbers \(\mathbb{R}\).
- The range of \(cos(x)\) is all values between \(-1\) and \(1\) included: \(-1 \leq cos(x) \leq 1\).
- The range of \(sin(x)\) is all values between \(-1\) and \(1\) included: \(-1 \leq sin(x) \leq 1\).
- The period of \(cos(x)\) and \(sin(x)\) is \(T = 360^{\circ}\).
-
Answer "true" or "false" to each of the following statements:
- \(sin(x+360) = sin(x)\) : true!
- \(cos(x+180) = -cos(x)\): true!
-
\(cos(x-360) = -cos(x)\): false!
In fact \(cos(x-360) = cos(x)\), since \(cos(x)\) is periodic with period \(T = 360^{\circ}\). -
\(sin(-x) = sin(x)\): false!
In fact \(sin(-x) = -sin(x)\). - \(cos(-x) = cos(x)\): true!
- \(sin(30) = sin(150) = -sin(210) = -sin(330)\): true!
- \(cos(45) = cos(315)\): true!
Exercise 2
Without using a calculator, find the exact value of each of the following angles:
- \(sin(-30)\)
- \(cos(120)\)
- \(sin(120)\)
- \(cos(270)\)
- \(sin(210)\)
- \(cos(-210)\)
- \(sin(135)\)
- \(cos(225)\)
- \(sin(-150)\)
- \(cos(330)\)
Answers Without Working
- \(sin(-30) = - \frac{1}{2}\)
- \(cos(120) = - \frac{1}{2}\)
- \(sin(120) = \frac{\sqrt{3}}{2}\)
- \(cos(270) = 0\)
- \(sin(210) = - \frac{1}{2}\)
- \(cos(-210) = - \frac{\sqrt{3}}{2}\)
- \(sin(135) = \frac{\sqrt{2}}{2}\)
- \(cos(225) = -\frac{\sqrt{2}}{2}\)
- \(sin(-150) = -\frac{1}{2}\)
- \(cos(330) = \frac{\sqrt{3}}{2}\)