RadfordMathematics.com

Quadratic Functions & Parabola

Quadratic functions are all of the form: \[f(x) = ax^2+bx+c\] where \(a\), \(b\) and \(c\) are known as the quadratic's coefficients and are all real numbers, with \(a\neq 0\).

The Parabola

Given a quadratic function \(f(x) = ax^2+bx+c\), it is described by its curve: \[y = ax^2+bx+c\] This type of curve is known as a parabola. A typical parabola is shown here:

Parabola, with equation \(y=x^2-4x+5\).

Concave-Up & Concave-Down: the Role of \(a\)

Given a parabola \(y=ax^2+bx+c\), depending on the sign of \(a\), the \(x^2\) coefficient, it will either be concave-up or concave-down:

  • \(a>0\): the parabola will be concave-up
  • \(a<0\): the parabola will be concave-down

We illustrate each of these two cases here:

The parabola \(y=2x^2 - 12x+9\).
The \(x^2\) coefficient is \(2\), which is positive.
This corresponds to the \(a>0\) scenario stated above.
The parabola is shown here:

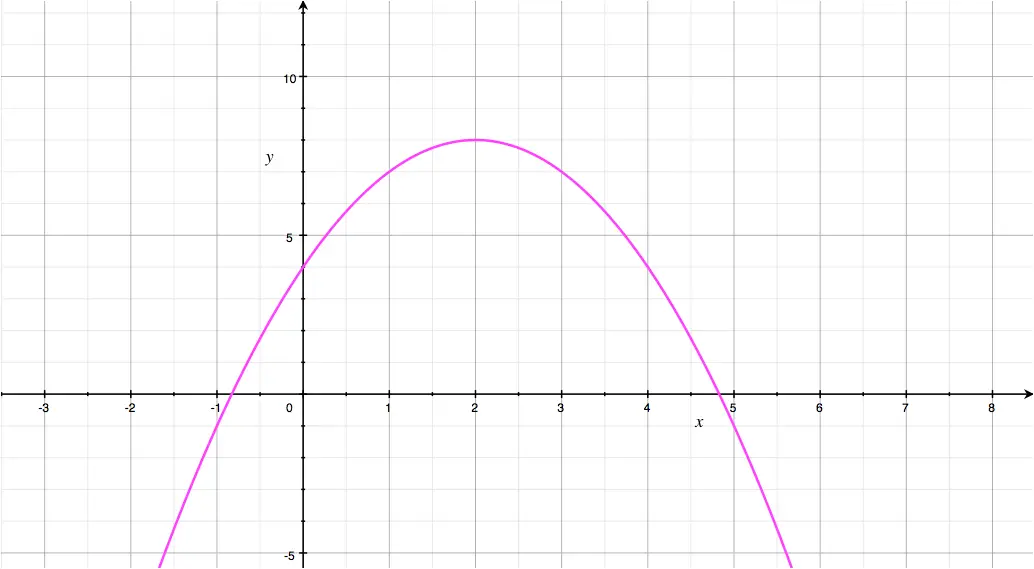
Concave-Up Parabola, "happy parabola".

The parabola \(y=-x^2 +4x + 4\).
The \(x^2\) coefficient is \(-1\), which is negative.
This corresponds to the \(a< 0\) scenario stated above.
The parabola is shown here:

Concave-Down Parabola, "unhappy parabola".

\(y\)-intercept, \(c\)

Given a parabola \(y=ax^2+bx+c\), the point at which it cuts the \(y\)-axis is known as the \(y\)-intercept.

The \(y\)-intercept will always have coordinates: \[\begin{pmatrix}0,c\end{pmatrix}\] where \(c\) is the only term in the parabola's equation without an \(x\).

Example

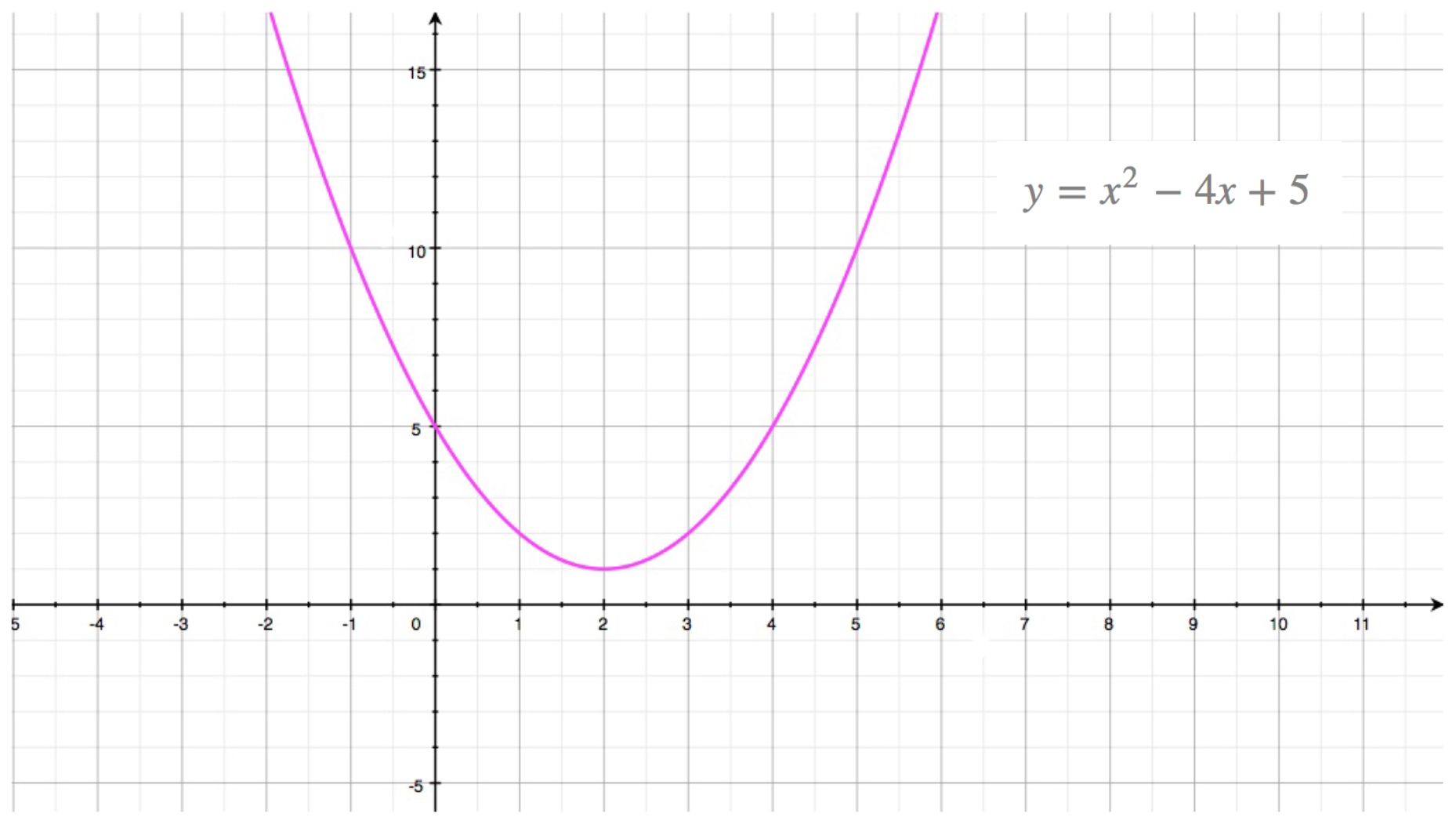
The parabola defined by: \[y = x^2+2x-3\] has \(y\)-intercept at: \[\begin{pmatrix}0,-3\end{pmatrix}\] Where \(-3\) is the only term without an \(x\) in the parabola's equation.

This can be seen on this parabola's graph:

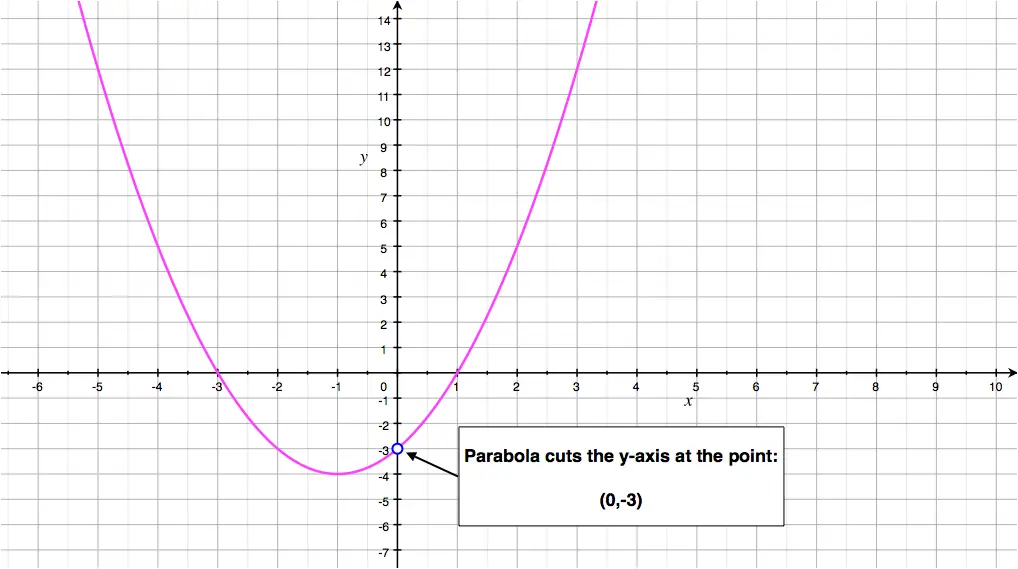
We can see that \(y=x^2+2x-3\) cuts the \(y\)-axis at the point \(\begin{pmatrix}0,-3 \end{pmatrix}\).

This can be confirmed algebraically we can find the \(y\)-intercept using the fact that when the curve cuts the \(y\)-axis: \(x=0\), so replacing \(x\) by \(0\) in the parabola's equation leads to: \[y = 0^2+2\times 0-3 = -3\] So the \(y\)-intercept is \(\begin{pmatrix}0,-3 \end{pmatrix}\).

Axis of Symmetry

All parabola have a vertical axis of symmetry, with equation: \[x = \frac{-b}{2a}\]

Tutorial: Axis of Symmetry

In the following tutorial we see how to use the formula for finding a parabola's axis of symmetry.




Example

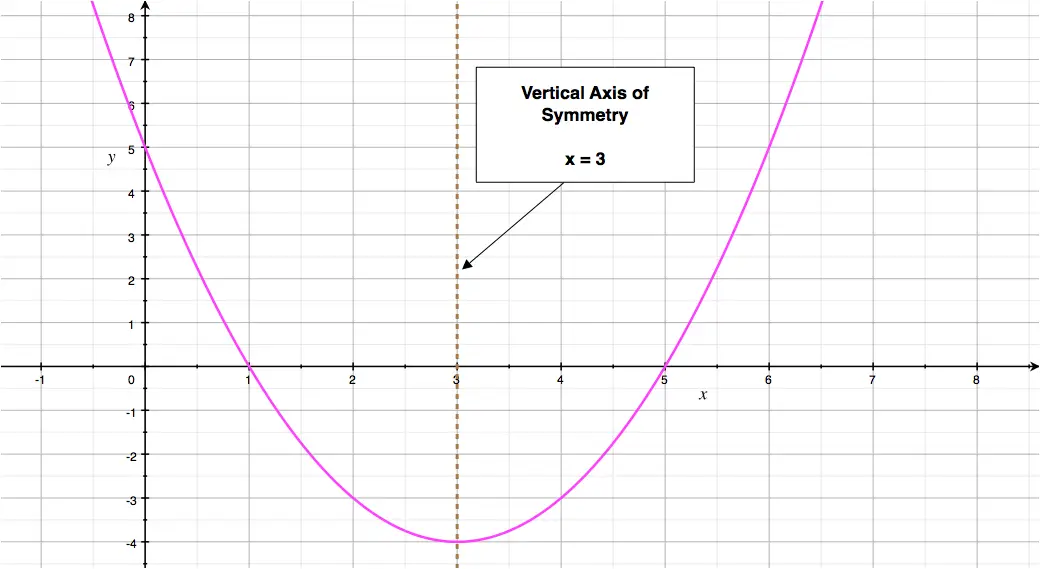
The parabola defined by: \[y = x^2 - 6x+5\] has axis of symmetry: \[\begin{aligned} x & = \frac{-(-6)}{2\times 1} \\ & = \frac{6}{2} \\ x & = 3 \end{aligned}\] This parabola's vertical axis of symmetry has equation: \[x = 3\] This is illustrated in the graph we see here, where the axis of symmetry is the dotted line.

Vertex of a Parabola

Given a quadratic function \(f(x) = ax^2+bx+c\), depending on the sign of the \(x^2\) coefficient, \(a\), its parabola has either a minimum or a maximum point:

  • if \(a>0\): it has a maximum point
  • if \(a<0\): it has a minimum point
in either case the point (maximum, or minimum) is known as a vertex.

Finding the Vertex

To find the vertex we calculate its \(x\)-coordinate, \(h\), with the formula given below.
We then calculate its \(y\)-coordinate, \(k\), by plugging in the

  • Step 1: calculate the \(x\)-coordinate of the vertex, \(h\), using the formula: \[h = \frac{-b}{2a}\]
  • Step 2: calculate the \(y\)-coordinate of the vertex, \(k\), by replacing \(x\) inside \(y=ax^2+bx+c\) and calculating the value of \(y\).

Tutorial: Coordinates of the Vertex

In the following tutorial we learn how to find the coordinates of a parabola's vertex, in other words the coordinates of its maximum, or minimum, point.




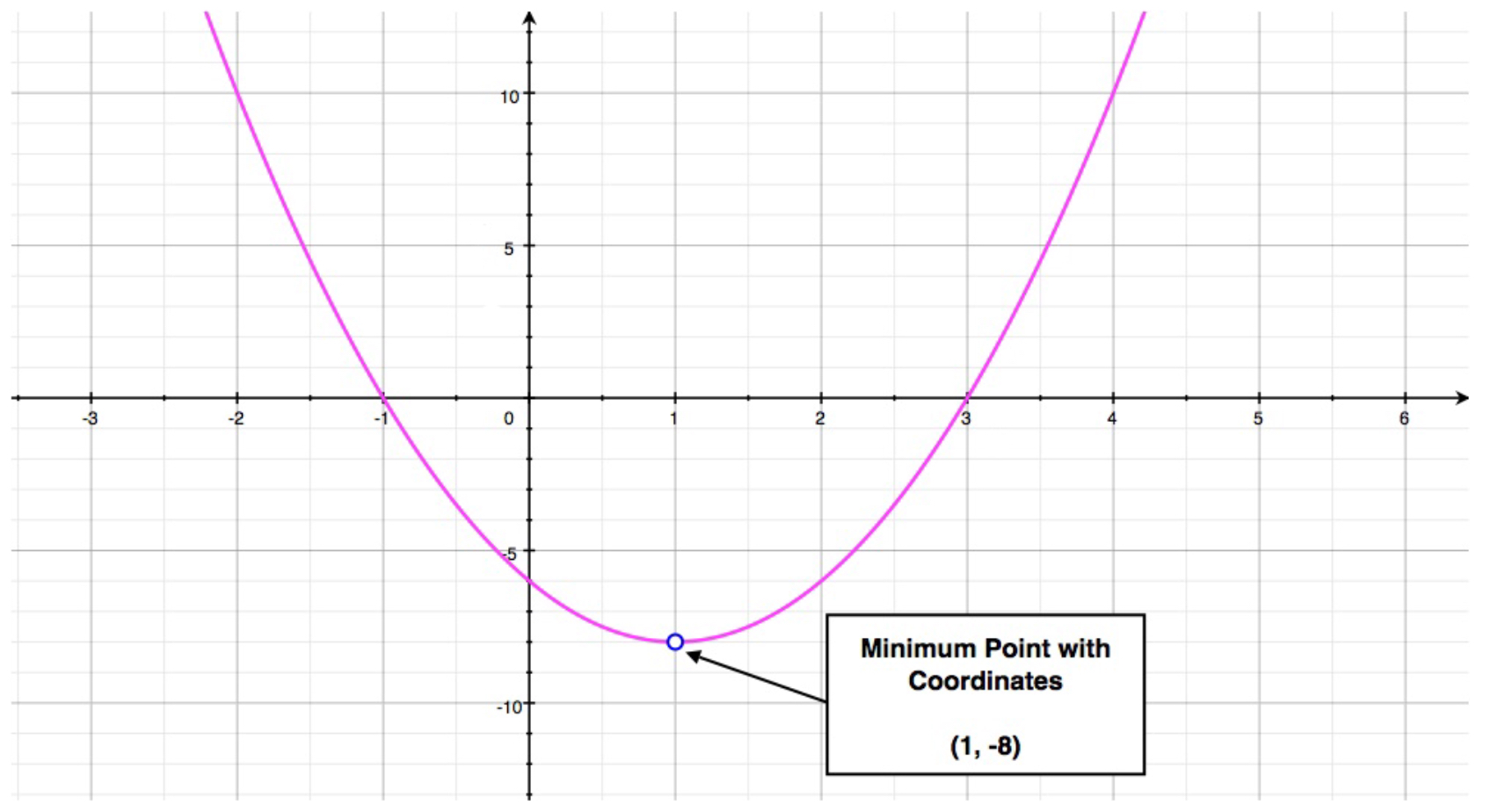
Example

Consider quadratic function whose parabola is described by: \[y = 2x^2 - 4x - 6\]

  1. State whether this parabola's vertex is a maximum, or a minimum.
  2. Find the coordinates of this parabola's vertex.

Solution

  1. The \(x^2\) coefficient is \(2\). Since \(2>0\) this parabola's vertex is a minimum point.
  2. To find the coordinates of the vertex, we follow the two steps we read further-up:
    • Step 1: we calculate the \(x\)-coordinate, \(h\), of the vertex using the formula: \[h = \frac{-b}{2a}\] Looking at \(y=2x^2 - 4x-6\), we see that: \[a = 2, \ b = -4, \ c = -6\] So the formula for the \(x\)-coordinate becomes: \[\begin{aligned} h & = \frac{-b}{2a}\\ & = \frac{-(-4)}{2\times 2} \\ & = \frac{4}{4} \\ h & = 1 \end{aligned}\] So the \(x\)-coordinate of the vertex is \(h=1\).
    • Step 2: we calculate the \(y\)-coordinate of the vertex by replacing \(x\) by \(1\) inside \(y=2x^2-4x-6\) and calculating the value of \(y\).

      That's: \[\begin{aligned} y & = 2\times 1^2-4\times 1-6 \\ & = 2\times 1 - 4 - 6 \\ & = 2 - 4 - 6 \\ & = -2 - 6 \\ y & = -8 \end{aligned}\] So the \(y\)-coordinate of the vertex is \(k=-8\).
    Finally we can state that this parabola has a minimum point with coordinates \(\begin{pmatrix}1, -8 \end{pmatrix}\).
This result is confirmed when we look at this parabola's graph. We can clearly see its vertex is a minimum point, with coordinates \(\begin{pmatrix}1, -8 \end{pmatrix}\):

Domain & Range

Domain

Given a quadratic function, \(f(x)=ax^2+bx+c\), and its parabola, \(y=ax^2+bx+c\), unless otherwise stated, the domain is:

All Real Numbers, \(\mathbb{R}\).
We can write this as: \[\text{Domain} = \mathbb{R}\]

Range

The range depends on two things:

  • the sign of the coefficient \(a\).
  • the \(y\)-coordinate, \(k\), of the vertex.
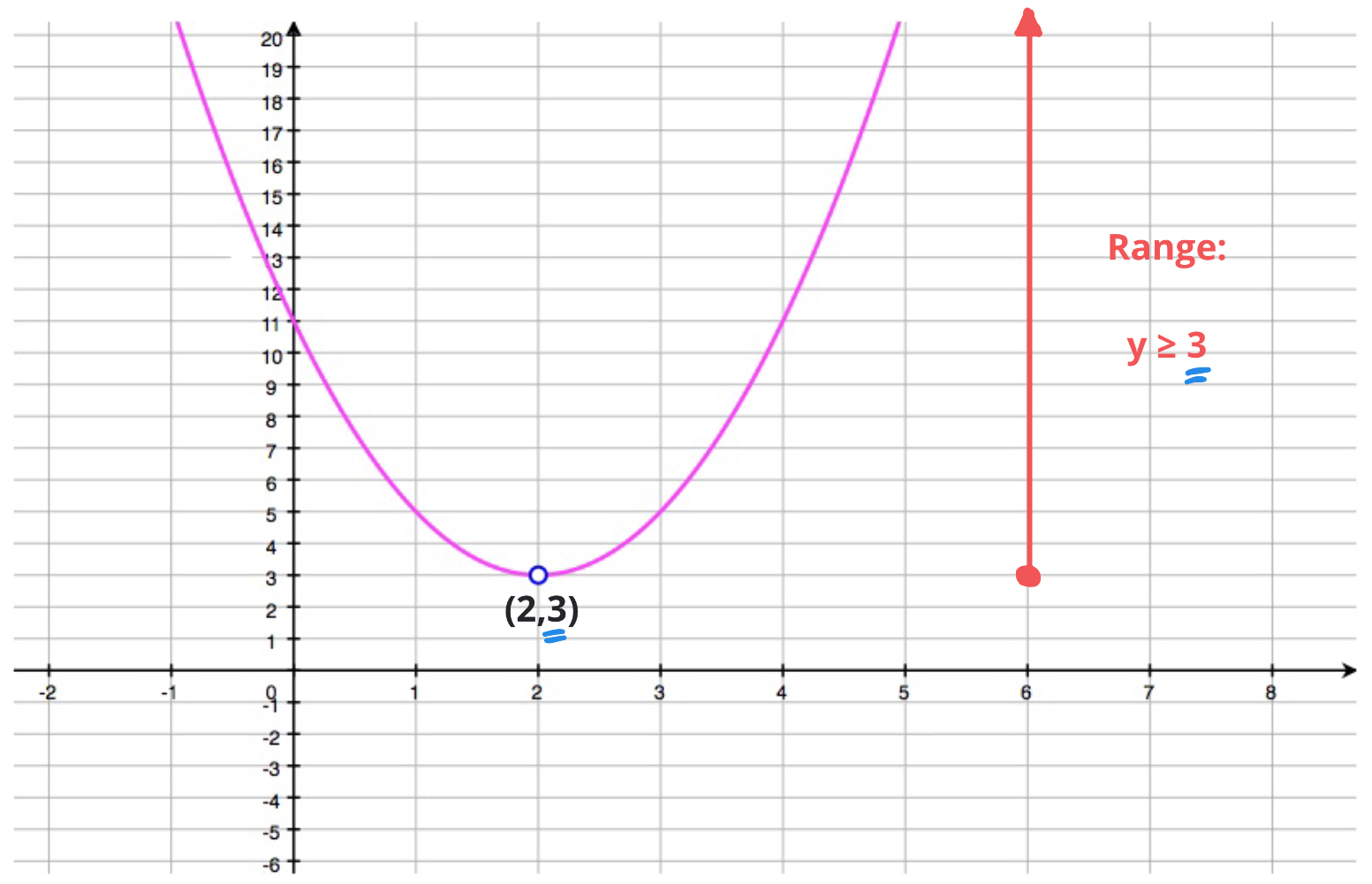
  • if \(a>0\): the parabola's vertex is a minimum point and the range will be: \[\text{Range}: y\geq k\]
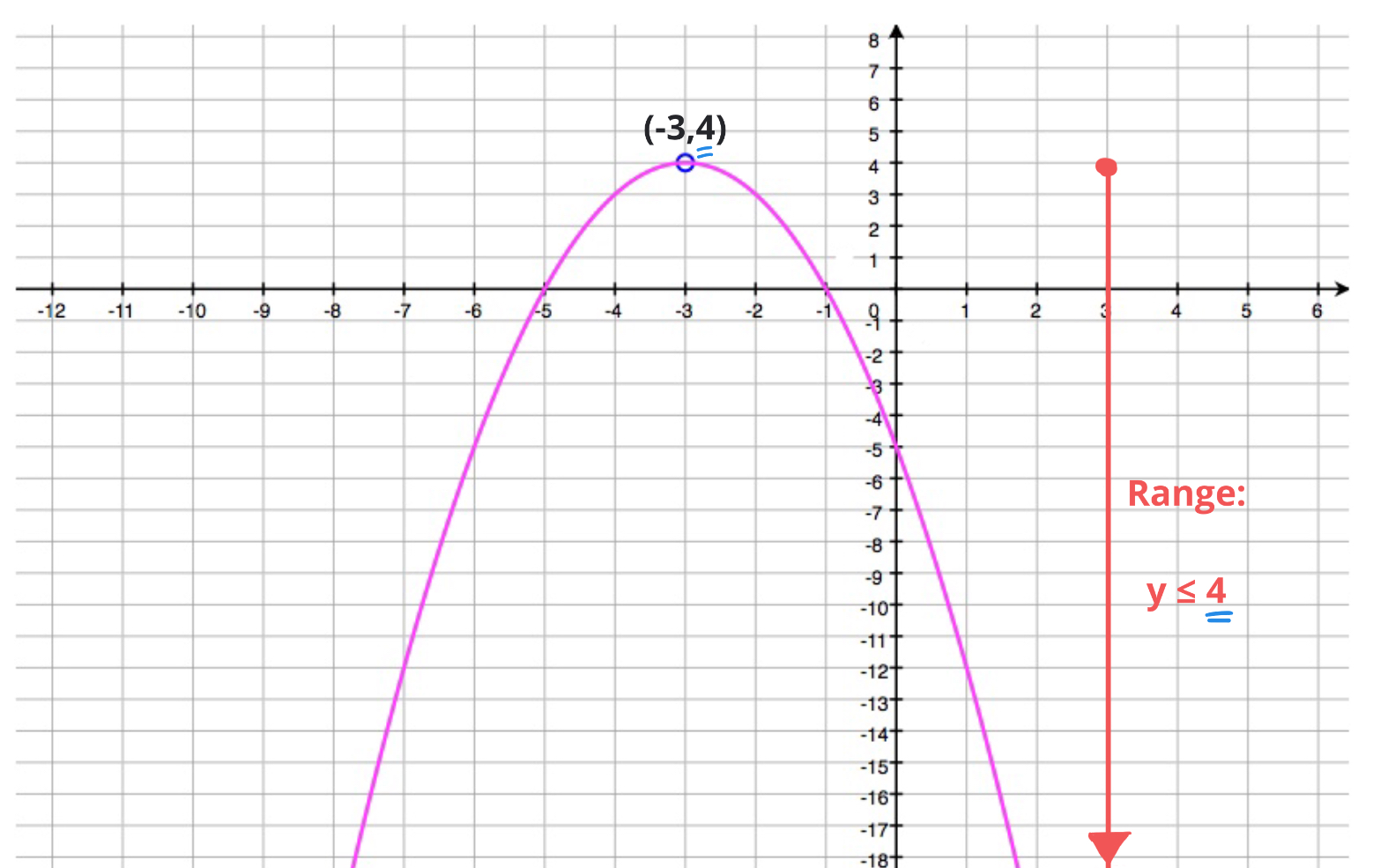
  • if \(a< 0\): the parabola's vertex is a maximum point and the range will be: \[\text{Range}: y\leq k\]

Example

Find the range of each of the quadratic functions defined by:

  1. The parabola \(y = 2x^2 - 8x+11\)
  2. The parabola \(y = -x^2 - 6x - 5\)

Solution

  1. To find the range, we find the coordinates of the vertex of \(y = 2x^2 - 8x+11\) (either using a graphical calculator, or algebraically).
    We find that the parabola has a minimum point with coordinates \(\begin{pmatrix}2,3\end{pmatrix}\).
    This can be seen on the parabola shown here:
    Since the parabola is concave-up, the range is: \[\text{Range}: \ y \geq 3\]

  2. To find the range, we find the coordinates of the vertex of \(y = -x^2 - 6x - 5\) (either using a graphical calculator, or algebraically).
    We find that the parabola has a maximum point with coordinates \(\begin{pmatrix}-3,4\end{pmatrix}\).
    This can be seen on the parabola shown here:
    Since the parabola is concave-down, the range is: \[\text{Range}: \ y \leq 4\]

\(x\)-intercepts

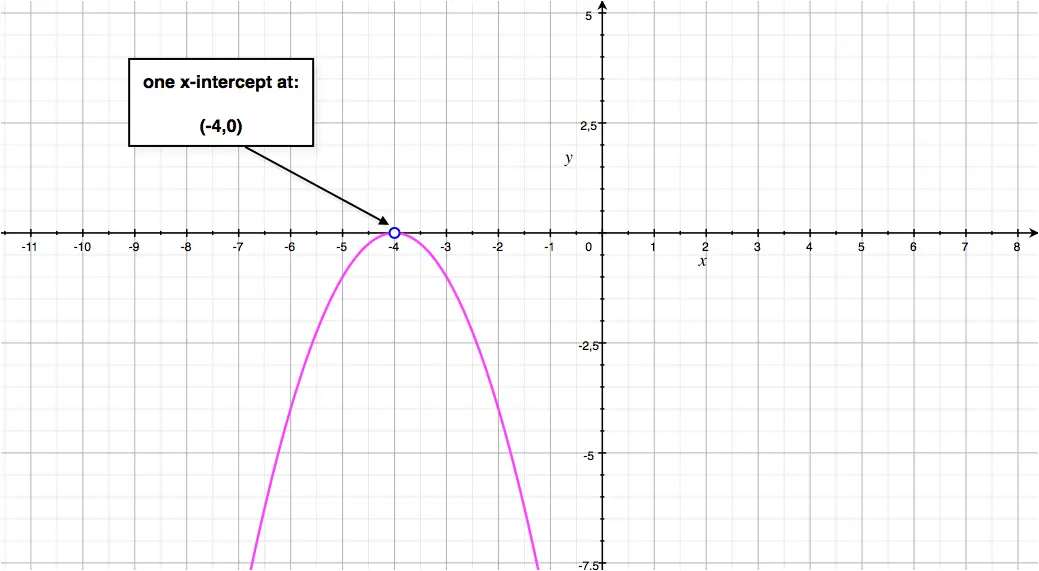
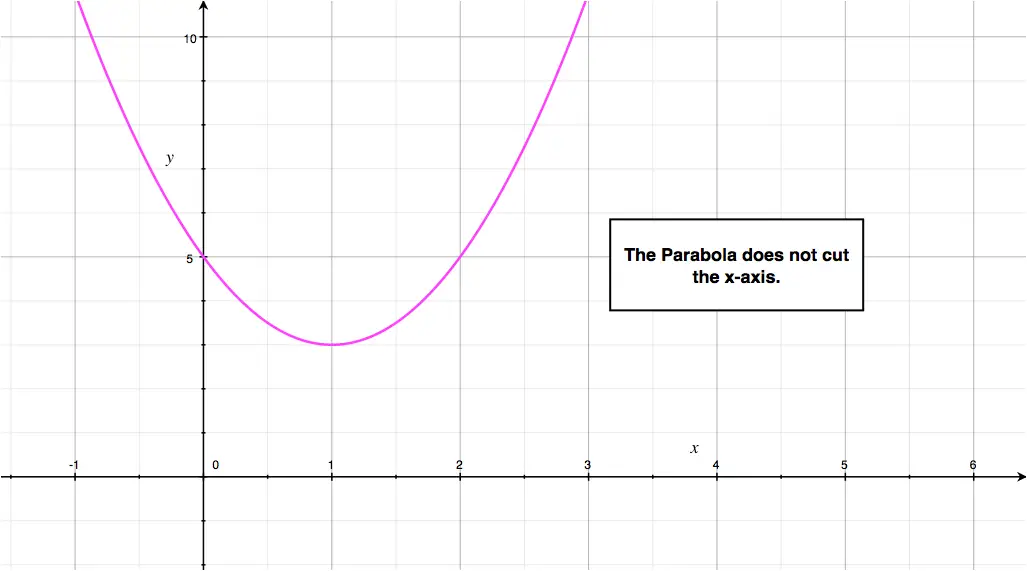
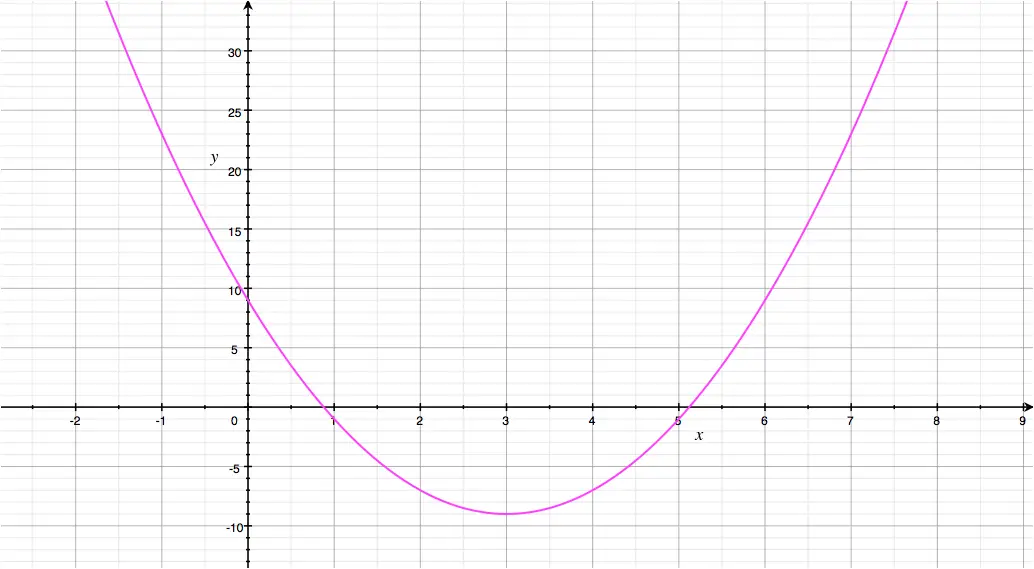
Given a quadratic function \(f(x) = ax^2+bx+c\), its parabola \(y=ax^2+bx+c\) cuts the \(x\)-axis either:

  • Twice
  • Once
  • Not at all
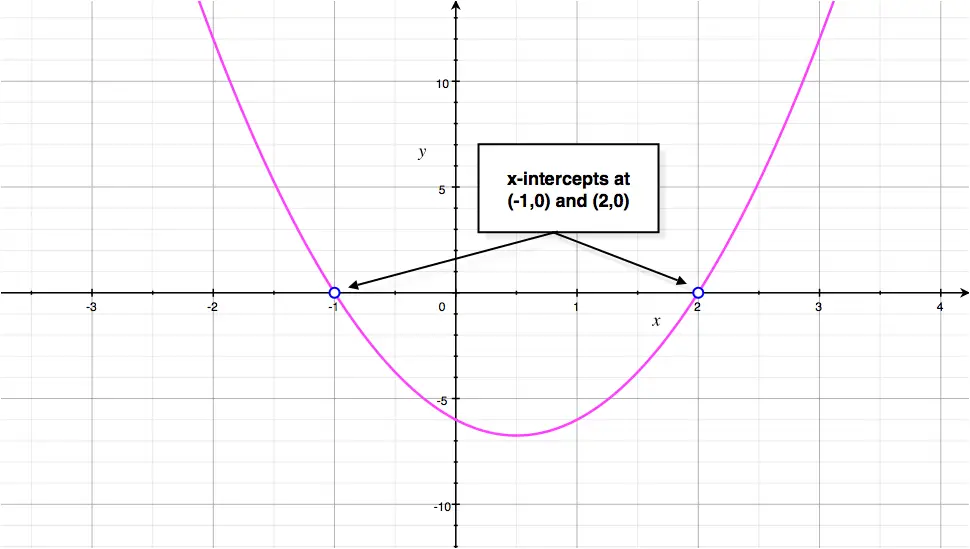
The \(x\)-values at which the curve cuts the \(x\)-axis are found by solving the quadratic equation: \[ax^2+bx+c = 0\] If you're unsure of how to solve this type of equation, make sure to read through our notes on the quadratic formula.

Example

Find the \(x\)-intercept(s) for each of the following parabola:

  1. \(y = 3x^2 - 3x-6\)
  2. \(y = -x^2-8x-16\)
  3. \(y = 2x^2-4x+5\)

Solution

  1. The parabola \(y = 3x^2 - 3x-6\) cuts the \(x\)-axis when \[3x^2-3x-6 = 0\] We solve this equation in two steps
    • Step 1: calculate the discriminant \(\Delta \): \[\begin{aligned} \Delta & = b^2 - 4ac\\ & = (-3)^2-4\times 3\times (-6)\\ & = 9 - 12 \times (-6) \\ & = 9 - (-72)\\ & = 9 + 72 \\ \Delta & = 81 \end{aligned}\]
    • Step 2: we now solve the equation, according to the sign of \(\Delta\).

      Since \(\Delta >0\) the equation has two solutions, given by the formula: \[x = \frac{-b\pm \sqrt{\Delta}}{2a}\] replacing \(\Delta\), \(a\) and \(b\) by their respective values leads to: \[\begin{aligned}x &= \frac{-b\pm \sqrt{\Delta}}{2a} \\ & = \frac{-(-3) \pm \sqrt{81}}{2\times 3} \\ & = \frac{3 \pm 9}{6} \\ x & = \frac{1 \pm 3}{2} \\ \end{aligned}\] So the equation \(3x^2 - 3x-6 = 0\) has two solutions: \[\begin{aligned} x & = \frac{1 - 3}{2} \\ & = \frac{-2}{2} \\ x & = -1 \end{aligned}\]
      and
      \[\begin{aligned} x & = \frac{1 + 3}{2} \\ & = \frac{4}{2} \\ x & = 2 \end{aligned}\] The solutions are \(x = -1\) and \(x = 2\).
    This means that the parabola cuts the \(x\)-axis twice, at: \[x = \begin{pmatrix}-1,0\end{pmatrix}\]
    and
    \[x = \begin{pmatrix}2,0\end{pmatrix}\] These two points are known as the parabola's \(x\)-intercepts.
    Looking at the parabola \(y = 3x^2 - 3x-6\) on an \(xy\)-grid we can confirm these results:
  2. The parabola \(y = -x^2-8x-16\) cuts the \(x\)-axis when: \[-x^2-8x-16 = 0\] We solve this equation in two-steps:
    • Step 1: calculate the discriminant \(\Delta \): \[\begin{aligned} \Delta & = b^2 - 4ac\\ & = (-8)^2-4\times (-1)\times (-16\) \\ & = 64 - (-4)\times (-16)\\ & = 64 - 64 \\ \Delta & = 0 \end{aligned}\]
    • Step 2: we now solve the equation, according to the sign of \(\Delta\).

      Since \(\Delta = 0\) the equation has one solution, given by the formula: \[x = \frac{-b}{2a}\] replacing \(a\) and \(b\) by their respective values leads to: \[\begin{aligned} x & = \frac{-b}{2a} \\ & = \frac{-(-8)}{2\times (-1)} \\ & = \frac{8}{-2} \\ x & = -4 \end{aligned}\] The solution to this equation is \(x = -4\).
    This means that the parabola cuts the \(x\)-axis once, at: \[x = \begin{pmatrix}-4,0\end{pmatrix}\] This point is the parabola's \(x\)-intercept.
    Looking at the parabola \(y = -x^2-8x-16\) on an \(xy\)-grid we can confirm this result:
  3. The parabola \(y = 2x^2-4x+5\) cuts the \(x\)-axis when: \[2x^2-4x+5 = 0\] We solve this equation in two-steps:
    • Step 1: calculate the discriminant \(\Delta \): \[\begin{aligned} \Delta & = b^2 - 4ac\\ & = (-4)^2 - 4\times 2\times 5 \\ & = 16 - 8 \times 5 \\ & = 16 - 40 \\ \Delta & = -24 \end{aligned}\]
    • Step 2: we now solve the equation, according to the sign of \(\Delta\).

      Since \(\Delta < 0\) the equation has no real solution
    This means that the parabola does not cut/touch the \(x\)-axis.
    Looking at the parabola \(y = 2x^2-4x+5\) on an \(xy\)-grid we can confirm this result: