Root Factoring Quadratics
(finding the equation of a parabola)
In this section we learn how to find the equation of a parabola, using root factoring.
Given the graph a parabola such that we know the value of:
- its two \(x\)-intercepts (the two points at which the parabola cuts the \(x\)-axis), or
- its single \(x\)-intercept, if the parabola only cuts the \(x\)-axis once
By the end of this section we'll know how to find the equation of any of the parabola shown here:
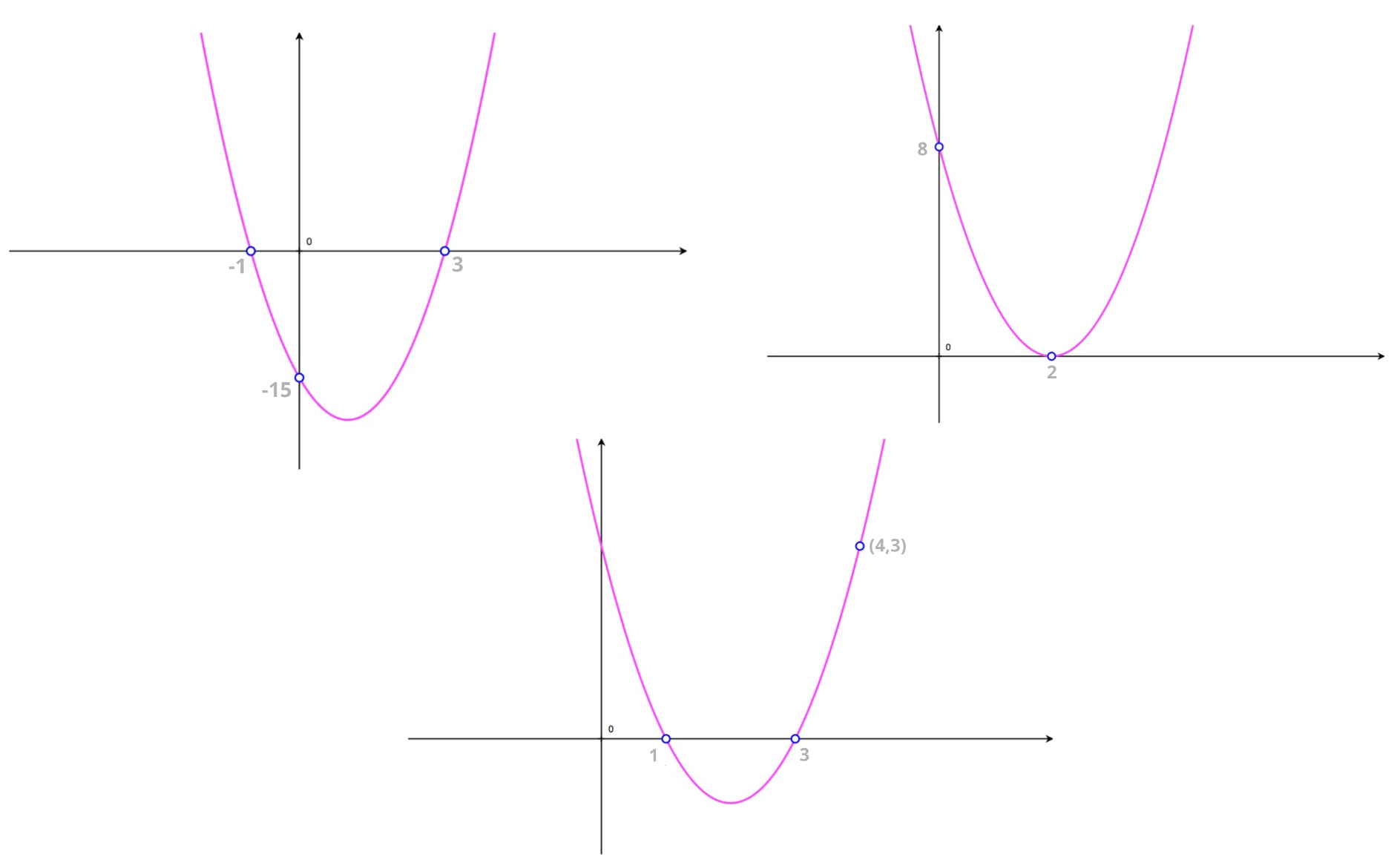
We start by learning how to write a parabola's equation in root factored form when the parabola has two \(x\)-intercepts as well as watch a couple of detailed tutorials showing us how this can be used to find a parabola's equation.
We'll then learn about the scenario in which the parabola has one \(x\)-intercept, which we'll also illustrate with a detailed tutorial.

Root Factored Form: two \(x\)-intercepts
If a parabola cuts the \(x\)-axis in two points: \[\begin{pmatrix}p,0\end{pmatrix} \quad \text{and} \quad \begin{pmatrix}q,0\end{pmatrix}\] then the parabola's equation, \(y=ax^2+bx+c\), can be written: \[y = a\begin{pmatrix}x - p \end{pmatrix}\begin{pmatrix}x - q \end{pmatrix}\] where \(p\) and \(q\) are the \(x\)-coordinates of the points at which the parabola cuts the \(x\)-axis (the \(x\)-intercepts).
Finding a Parabola's Equation
Given the graph of a parabola, like either of the two shown here, we can use root factoring to find their parabola's equations.
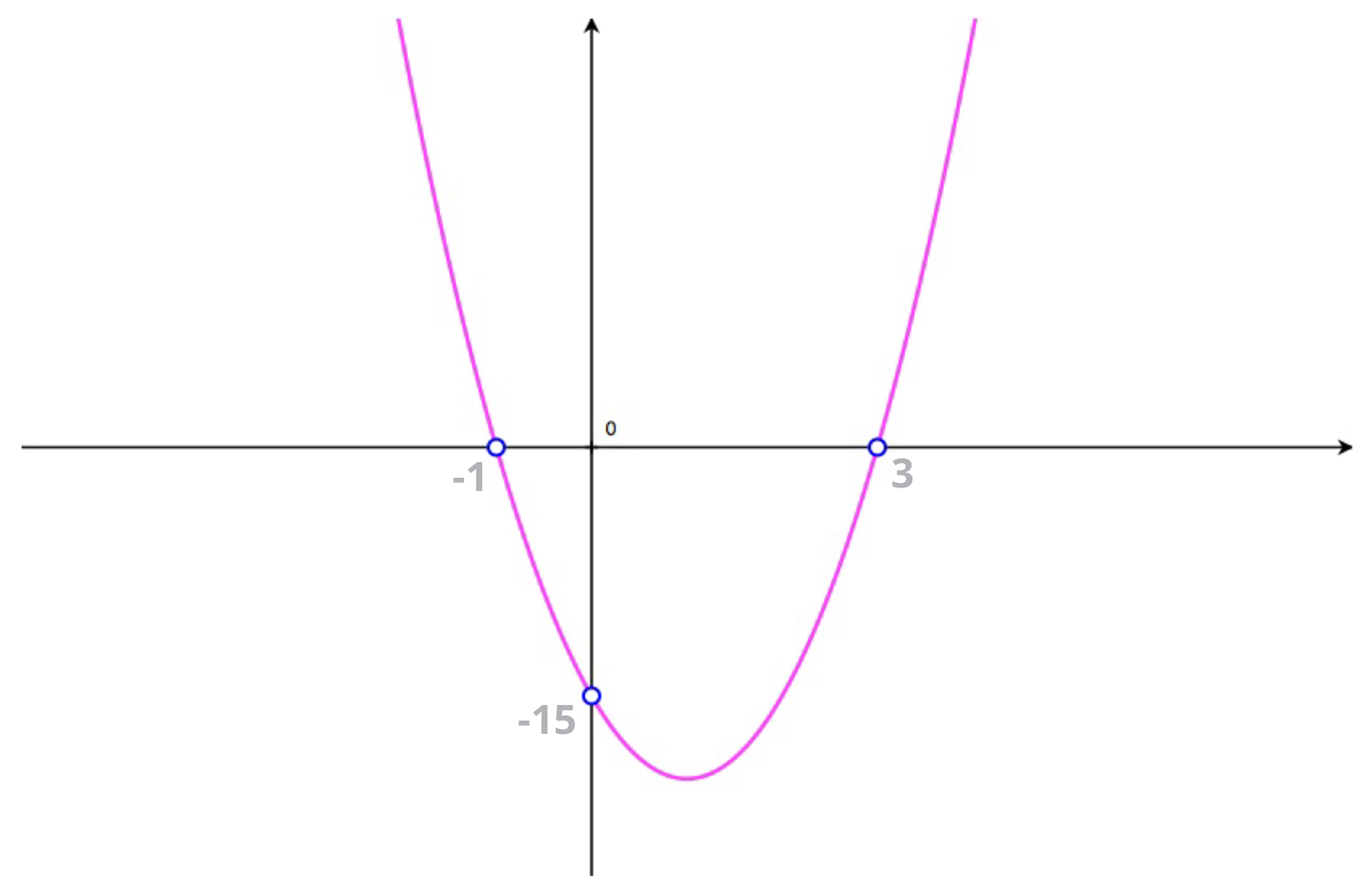
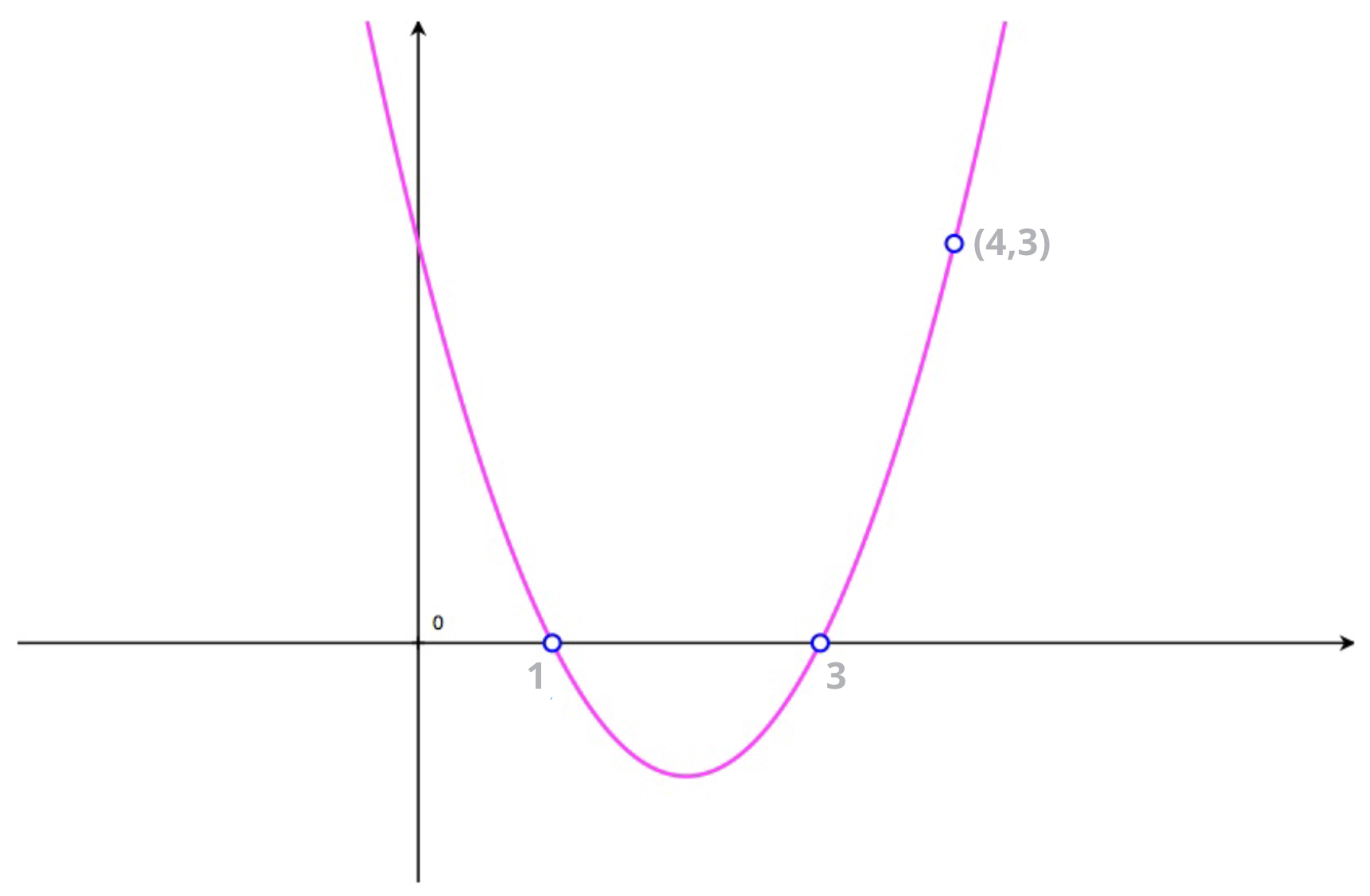
Note: notice that in each these graphs we can see both:
- the \(x\)-intercepts, and
- the coordinates of one other point the curve passes through.
The method for finding a parabola's equation, when given a graph like those we have here, is clearly explained in the following tutorials, make sure to watch them now.
Tutorial 1
In this first tutorial we learn how to find the equation of a parabola given:
- it cuts the \(x\)-axis in two points, that we are given or can read from the graph
- we know the value of the parabola's \(y\)-intercept.
Tutorial 2
In this second tutorial we learn how to find the equation of a parabola given:
- it cuts the \(x\)-axis in two points, that we are given or can read from the graph
- we know the coordinates of one other point through which the parabola passes (other than the \(y\)-intercept).
Exercise 1
Use root factoring to find the equation of each of the parabola shown below.
In each case, write the parabola's equation in root factored form and in the general \(y=ax^2+bx+c\) form.
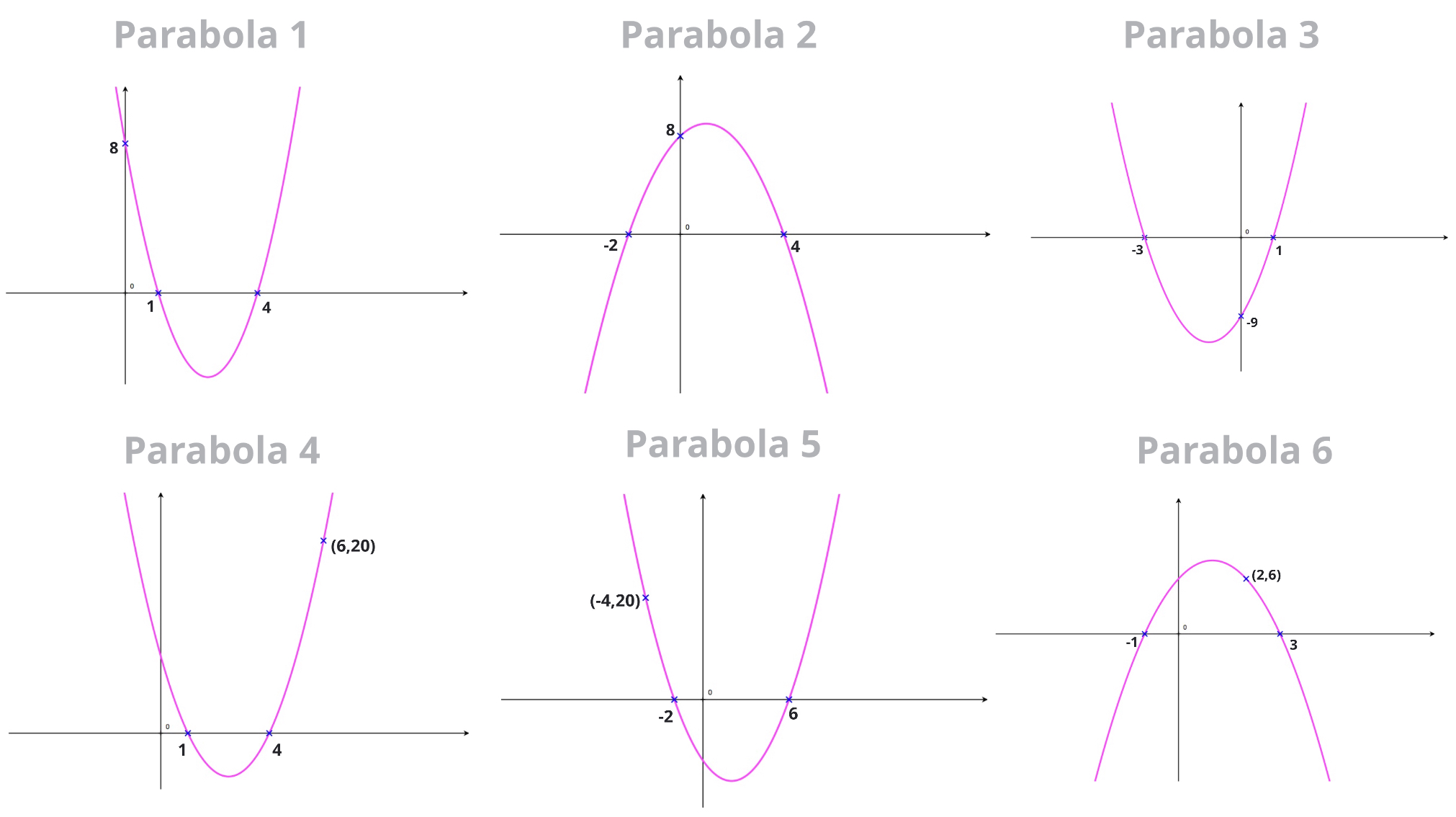
Answers Without Working
-
We find:
\[y=2(x-1)(x-4)\]
and so: \[y = 2x^2-10x+8\] -
We find:
\[y=-(x+2)(x-4)\]
and so: \[y = -x^2+2x+8\] -
We find:
\[y=3(x+3)(x-1)\]
and so: \[y = 3x^2+6x-9\] -
We find:
\[y=2(x-1)(x-4)\]
and so: \[y = 2x^2-10x+8\] -
We find:
\[y=(x+2)(x-6)\]
and so: \[y = x^2-4x-12\] -
We find:
\[y=-2(x+1)(x-3)\]
and so: \[y = -2x^2+4x+6\]
Root Factored Form: one \(x\)-intercept
If a parabola cuts the \(x\)-axis in one point: \[\begin{pmatrix}p,0\end{pmatrix}\] then the parabola's equation, \(y=ax^2+bx+c\), can be written: \[y = a\begin{pmatrix}x - p \end{pmatrix}^2\] where \(p\) is the \(x\)-coordinate of the point at which the parabola cuts the \(x\)-axis (the \(x\)-intercept).
Tutorial 3
In this third tutorial we learn how to find the equation of a parabola given:
- it cuts/tcouhes the \(x\)-axis in only one point
- we know the coordinates of one other point through which the parabola passes.
Exercise 2
Use root factoring to find the equation of each of the parabola shown below.
In each case, write the parabola's equation in root factored form and in the general \(y=ax^2+bx+c\) form.
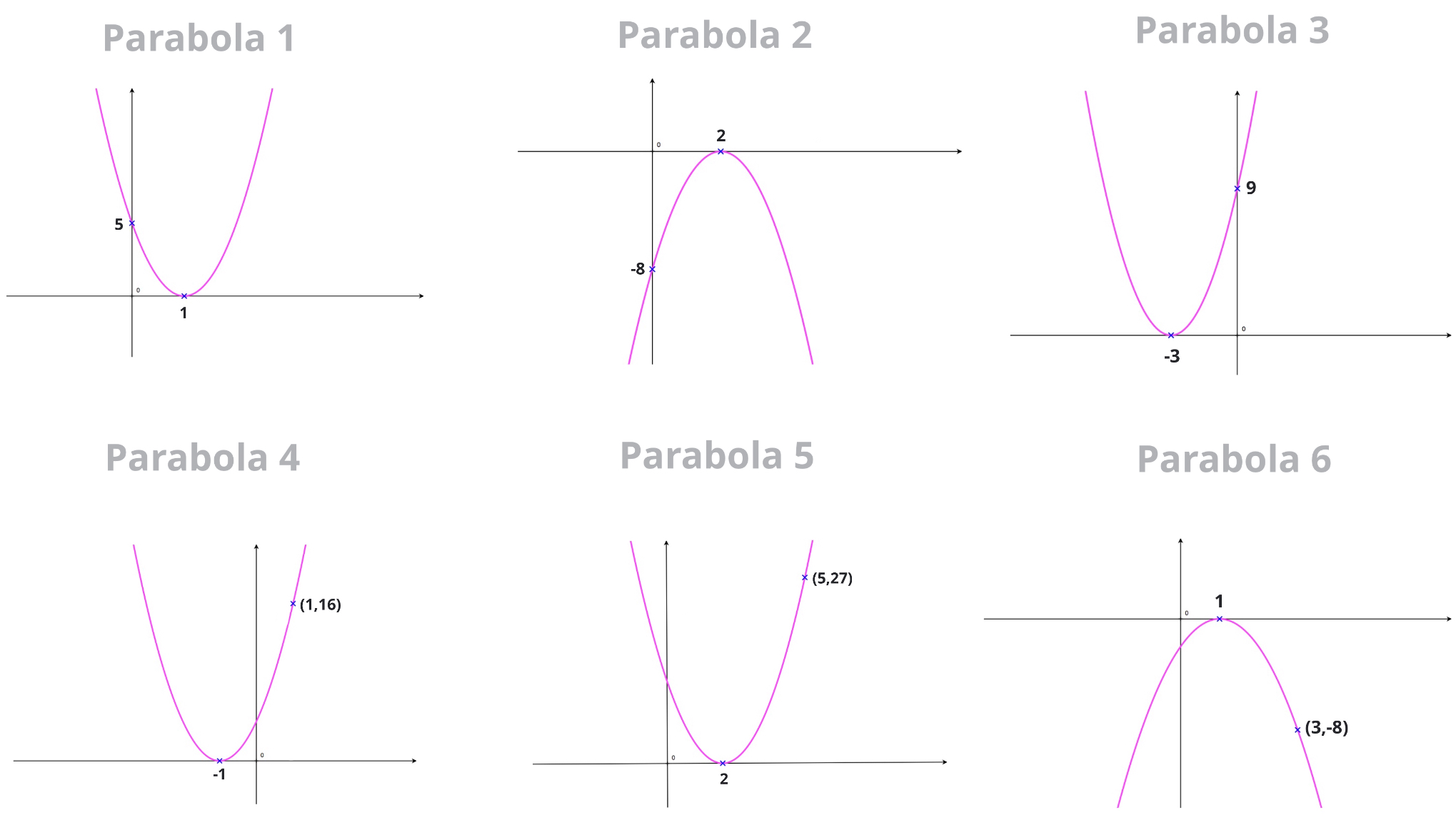
Answers Without Working
-
We find:
\[y=5(x-1)^2\]
and so: \[y = 5x^2-10x+5\] -
We find:
\[y=-2(x-2)^2\]
and so: \[y = -2x^2+8x-8\] -
We find:
\[y=(x+3)^2\]
and so: \[y = x^2+6x+9\] -
We find:
\[y=4(x+1)^2\]
and so: \[y = 4x^2+8x+4\] -
We find:
\[y=3(x-2)^2\]
and so: \[y = 3x^2-12x+12\] -
We find:
\[y=-2(x-1)^2\]
and so: \[y = -2x^2+4x-2\]