RadfordMathematics.com

Parameters of Discrete Random Variables

(How to Find the Mean, Median, Mode, Variance & Standard Deviation of a Discrete Random Variable)

In this section we learn how to find the , mean, median, mode, variance and standard deviation of a discrete random variable.

We define each of these parameters:

  • mode
  • mean (expected value)
  • variance & standard deviation
  • median
in each case the definition is given and we illustrate how to calculate its value with a tutorial, worked examples as well as some exercises all of which are solved in short video tutorials.

It is worth spending a bit of time on this section as all that is taught here applies to all discrete random variable probability distributions, such as the Binomial Distribution as well as the Poisson Distribution.

Mode

Given a discrete random variable \(X\), its mode is the value of \(X\) that is most likely to occur.
Consequently, the mode is equal to the value of \(x\) at which the probability distribution function, \(P\begin{pmatrix}X = x \end{pmatrix}\), reaches a maximum.

Example

A discrete random variable \(X\)can take-on the values: \[x = \left \{ 2, \ 3, \ 4, \ 5, \ 6 \right \}\] and has probability distribution function: \[P\begin{pmatrix} X = x \end{pmatrix} = \frac{x^2}{90}\]

  1. Construct the probability distribution table for \(X\).
  2. Find the mode of the discrete random variable.

Solution

  1. To construct the probability distribution table we calculate each of the probabilities \(P\begin{pmatrix}X = 2\end{pmatrix}\), \(P\begin{pmatrix}X = 3\end{pmatrix}\), ... , \(P\begin{pmatrix}X = 6\end{pmatrix}\) and summarize the results in a table like the one shown here:
  2. The discrete random variable's mode is the value that \(X\) is most likely to take-on.
    Looking at this table we can see that the greatest probability is \(P\begin{pmatrix}X = 6 \end{pmatrix} = \frac{36}{90}\).
    So the mode is \(6\).

Mean \(\mu \) (or Expected Value \(E\begin{pmatrix}X\end{pmatrix} \))

The expected value of a discrete random variable \(X\) is the mean value (or average value) we could expect \(X\) to take if we were to repeat the experiment a large number of times. It is calculated with: \[E(X) = \sum x.P \begin{pmatrix} X = x \end{pmatrix} \] The expected value is also known as the mean \(\mu \) of the random variable, in which case we write: \[\mu = \sum x.P \begin{pmatrix} X = x \end{pmatrix}\] Note: it doesn't matter whether we refer to \(E(X)\) or \(\mu \), but it is important to know that they both refer to the same thing.

Example

Consider the simple experiment of rolling a single unbiased dice once.
Define the discrete random variable \(X\) as: \[X:\text{the value obtained when rolling the dice}\] Find the mean value of this discrete random variable.

Solution

The discrete random variable \(X\) can take-on any of the \(\left \{ 1, \ 2, \ 3, \ 4, \ 5, \ 6 \right \}\).
We can illustrate this probability distribution in a table:

We now calculate the mean value \(\mu \) of \(X\): \[\begin{aligned} \mu & = \sum_{x=1}^6 x.P \begin{pmatrix} X = x \end{pmatrix} \\ & = 1 \times \frac{1}{6} + 2 \times \frac{1}{6} + 3 \times \frac{1}{6} + 4 \times \frac{1}{6} + 5 \times \frac{1}{6} + 6 \times \frac{1}{6} \\ & = \frac{21}{6} \\ \mu & = 3.5 \end{aligned}\] This mean tells us that if we were to roll a dice a large number of times and were to calculate the average of all the values we obtained the result would be close to \(3.5\). In other words the mean value we can expect to obtain when rolling a dice is \(3.5\).

Tutorial 1

In the following tutorial we show how to find the mode and the mean of a discrete random variable, using the rules we just read (above).

We do this for a discrete random variable \(X\) that has the following probability distribution table:

Exercise 1

  1. A discrete random variable \(X\) has the following probability distribution table:
    1. State the mode.
    2. Calculate this discrete random variable's mean value.
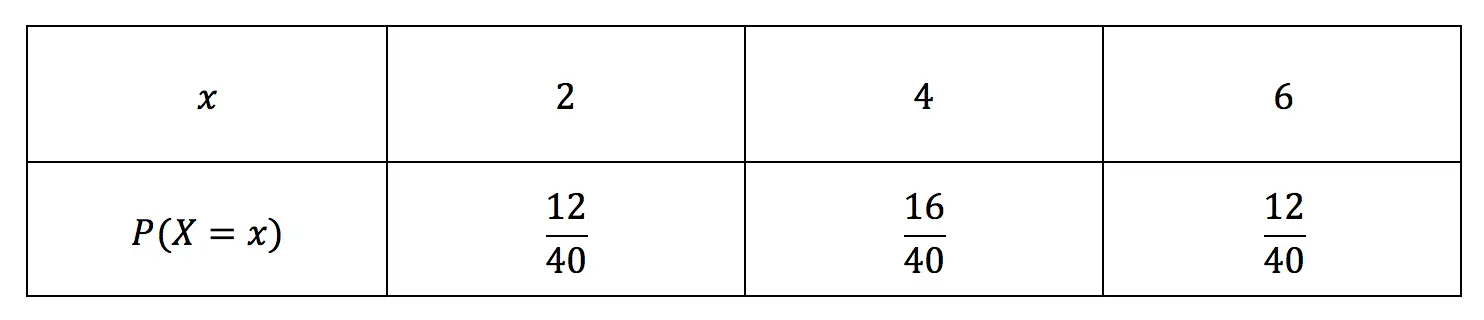
  2. A discrete random variable \(X\) can take on the values: \[x = \left \{ 2, \ 4, \ 6 \right \}\] and has probability distribution function defined as: \[P\begin{pmatrix} X = x \end{pmatrix} = \frac{8x - x^2}{40}\]
    1. Construct a probability distribution table for \(X\).
    2. State the mode of \(X\).
    3. Calculate this discrete random variable's mean value.
  3. A discrete random variable \(X\) has probability distribution table:
    1. Find the value of \(k\).
    2. State the mode of \(X\).
    3. Calculate the expected value \(E\begin{pmatrix}X\end{pmatrix}\).

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 1

Variance & Standard Deviation

Variance, \(Var\begin{pmatrix}X\end{pmatrix}\) or \(\sigma^2\)

Given a discrete random variable \(X\), we calculate its Variance, written \(Var\begin{pmatrix}X \end{pmatrix}\) or \(\sigma^2\), using one of the following two formula:

Formula 1

\[Var\begin{pmatrix}X \end{pmatrix} = \sum \begin{pmatrix}x - \mu \end{pmatrix}^2 . P\begin{pmatrix} X = x \end{pmatrix}\]

Formula 2
\[Var\begin{pmatrix} X \end{pmatrix} = E\begin{pmatrix}X^2 \end{pmatrix} - \mu^2\] Where: \[E\begin{pmatrix}X^2 \end{pmatrix} = \sum x^2.P\begin{pmatrix} X = x \end{pmatrix}\]

Standard Deviation, \(\sigma \)

The standard deviation, \(\sigma\), of a discrete random variable \(X\) tells us how far away from the mean \(\mu \) we can expect the value of \(X\) to be.
We calculate \(\sigma \) using the formula: \[\sigma = \sqrt{ Var \begin{pmatrix} X \end{pmatrix}}\] Note: it is important to realize and keep in mind that the value of \(\sigma \) is an average and could be expected to be observed after a sufficiently large number of trials.

Example

A discrete random variable \(X\) can take the values \(x = \left \{ 3, \ 4, \ 6, \ 7 \right \}\) and has a probability distribution function \(P\begin{pmatrix} X = x \end{pmatrix} = \frac{x}{20}\).

  1. Calculate the mean value of \(X\).
  2. Calculate the variance and the standard deviation.

Solution

  1. To calculate the mean value we use the formula: \[\mu = \sum x.P\begin{pmatrix}X = x \end{pmatrix}\] Given \(X\) can take-on either of the values \(3\), \(4\), \(6\) and \(7\), this formula leads to: \[\begin{aligned} \mu & = 3 \times P \begin{pmatrix} X = 3 \end{pmatrix} + 4\times \begin{pmatrix} X = 4 \end{pmatrix} + 6 \times \begin{pmatrix} X = 6 \end{pmatrix} + 7 \times \begin{pmatrix} X = 7 \end{pmatrix} \\ & = 3 \times \frac{3}{20} + 4 \times \frac{4}{20} + 6 \times \frac{6}{20} + 7 \times \frac{7}{20} \\ & = \frac{9}{20} + \frac{16}{20} + \frac{36}{20} + \frac{49}{20} \\ & = \frac{110}{20} \\ \mu & = 5.5 \end{aligned}\] Finally, we can state: the mean value of this discrete random variable is \(\mu = 5.5\).

  2. To calculate the variance we use the formula: \[Var\begin{pmatrix} X \end{pmatrix} = E\begin{pmatrix}X^2 \end{pmatrix} - \mu^2\] Where: \[E\begin{pmatrix} X^2 \end{pmatrix} = \sum x^2.P\begin{pmatrix} X = x \end{pmatrix}\] We start by calculating \(E\begin{pmatrix}X^2\end{pmatrix}\).
    Using the values \(x\) that the discrete random variable can take the formula leads to: \[\begin{aligned} E\begin{pmatrix} X^2 \end{pmatrix} & = 3^2\times P\begin{pmatrix}X = 3 \end{pmatrix} + 4^2 \times P\begin{pmatrix}X = 3 \end{pmatrix} + 6^2 \times P\begin{pmatrix}X = 6 \end{pmatrix} + 7^2 \times P\begin{pmatrix}X = 7 \end{pmatrix} \\ & = 3^2 \times \frac{3}{20} + 4^2 \times \frac{4}{20} + 6^2\times \frac{6}{20} + 7^2 \times \frac{7}{20} \\ & = 9 \times \frac{3}{20} + 16 \times \frac{4}{20} + 36 \times \frac{6}{20} + 49 \times \frac{7}{20} \\ & = \frac{27}{20} + \frac{64}{20} + \frac{216}{20} + \frac{343}{20} \\ & = \frac{650}{20} \\ E\begin{pmatrix} X^2 \end{pmatrix} & = 32.5 \end{aligned}\] Now that we know the value of \(E\begin{pmatrix} X^2 \end{pmatrix} = 32.5\), we can calculate the variance: \[\begin{aligned} Var\begin{pmatrix} X \end{pmatrix} = E\begin{pmatrix}X^2\end{pmatrix} - \mu^2 \\ & = 32.5 - 5.5^2 \\ & = 32.5 - 30.25 \\ Var\begin{pmatrix} X \end{pmatrix} & = 2.25 \end{aligned}\] The variance is \(2.25\).

    Now that we know the variance, we can calculate this discrete random variable's standard deviation: \[\begin{aligned} \sigma & = \sqrt{Var\begin{pmatrix} X \end{pmatrix}} \\ & = \sqrt{2.25}\\ \sigma & = 1.5 \end{aligned}\] Finally, we can state: the standard deviation is \(\sigma = 1.5\).

Tutorial 2

In tutorial 2 we learn how to calculate the variance and standard deviation of a discrete random variable.
We do this for the following example:

A discrete random variable \(X\) can take the values \(x = \left \{ 1, \ 2, \ 3, \ 4 \right \}\).
It has probability distribution function \(P\begin{pmatrix}X = x \end{pmatrix} = \frac{x}{10}\).

Find: the variance and the standard deviation of \(X\).

Exercise 2

  1. A discrete random variable \(X\) has probability distribution function defined as: \[P\begin{pmatrix} X = x \end{pmatrix} = \frac{x^2}{120}\] Where \(X\) can take-on the values \(1\), \(3\), \(5\), \(6\) and \(7\).
    1. Calculate this discrete random variable's mean value.
    2. Calculate the standard deviation.
  2. A discrete random variable \(X\) has the following probability distribution table:
    1. Calculate the mean value of \(X\).
    2. Calculate the variance of \(X\).
    3. Calculate the standard deviation of \(X\)
  3. A discrete random variable \(X\) can take-on the values: \[x = \left \{ 1, \ 2, \ 3, \ 4 \right \}\] and has probability distribution function: \[P\begin{pmatrix} X = x \end{pmatrix} = \frac{x}{10}\]
    1. Construct a probability distribution table for this discrete random variable.
    2. State its mode.
    3. Calculate the mean value of \(X\).
    4. Calculate the variance of \(X\), hence calculate its standard deviation.

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 2

Median

Given a discrete random variable \(X\) and its cumulative distribution function \(P\begin{pmatrix} X \leq x \end{pmatrix} = F(x)\), the median of the discrete random variable \(X\) is the value \(M\) defined as: \[M = \frac{x_1+x_2}{2}\] Where:

  • \(x_1\) is the greatest value \(X\) can take such that: \(P\begin{pmatrix}X \leq x_1 \end{pmatrix} \leq 0.5\).
  • \(x_2\) is the smallest value \(X\) can take such that: \(P\begin{pmatrix}X \leq x_2 \end{pmatrix} \geq 0.5\).

The median \(M\) of \(X\) is the middle value.
The probability that \(X\) takes-on a value less than \(M\) is \(0.5\). Similarly, the probability that \(X\) takes-on a value greater than \(M\) is \(0.5\).
In other words there is an equal chance that \(X\) be greater or less than \(M\).

Example

A discrete random variable \(X\) has the following cumulative probability distribution table:


Find the median value of \(X\).

Solution

We need to find \(x_1\) and \(x_2\).
Remember:

  • \(x_1\) is the greatest value \(X\) can take such that: \(P\begin{pmatrix}X \leq x_1 \end{pmatrix} \leq 0.5\).
  • \(x_2\) is the smallest value \(X\) can take such that: \(P\begin{pmatrix}X \leq x_2 \end{pmatrix} \geq 0.5\).
Looking at the cumulative distribution table we see that:
  • the greatest value of \(P\begin{pmatrix} X \leq x \end{pmatrix}\) that is less than, or equal to, \(0.5\) is \(P\begin{pmatrix} X \leq x \end{pmatrix} = 0.3\), which corresponds to \(X = 1\).
  • the smallest value of \(P\begin{pmatrix} X \leq x \end{pmatrix}\) that is greater than, or equal to, \(0.5\) is \(P\begin{pmatrix} X \leq x \end{pmatrix} = 0.6\), which corresponds to \(X = 2\).
So:
\(x_1 = 1\) and \(x_2 = 2\)
The median value of \(X\) is therefore: \[\begin{aligned} M &= \frac{x_1 + x_2}{2} \\ & = \frac{1+2}{2} \\ & = \frac{3}{2} \\ M & = 1.5 \end{aligned}\] The median value of \(X\) is \(1.5\), which tells us there is a \(50\%\) chance that \(X\) be less than \(1.5\) and a \(50\%\) chance it be greater than \(1.5\).

Tutorial 3

In the following tutorial we learn how to find the median of a discrete random variable.

We start by reminding ourselves how to construct a cumulative probability distribution table and then learn how to use it to find the median value.

For this we suppose we're given a discrete random variable \(X\) with the following probability distribution table:

Exercise 3

  1. A discrete random variable \(X\) has the following cumulative distribution table:
    1. Find \(P\begin{pmatrix}X = 4\end{pmatrix}\)
    2. Find the median value of \(X\).
  2. A discrete random variable \(X\) has probability distribution table defined as:
    1. Construct this random variable's cumulative distribution table.
    2. Find the median value of \(X\).
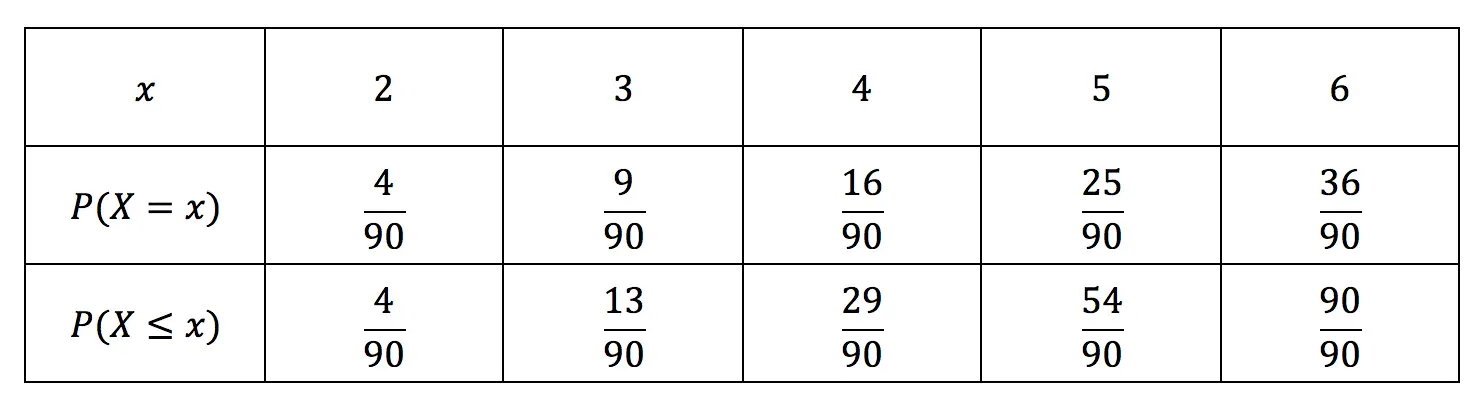
  3. Given the discrete random variable \(X\), with probability distribution function: \[P\begin{pmatrix}X = x \end{pmatrix} = \frac{x^2}{90}\] Where: \[x = \left \{ 2, \ 3, \ 4, \ 5, \ 6 \right \}\]
    1. Construct a probability distribution table for \(X\).
    2. State the mode of \(X\).
    3. Calculate the mean value of \(X\).
    4. Calculate this discrete ranom variable's standard deviation.
    5. Construct a cumulative distribution table for \(X\).
    6. Find the median value of \(X\).

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 3

Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.