RadfordMathematics.com

Complex Numbers

Introduction to Complex Numbers & Operations with Complex Numbers

In this section we learn about complex numbers. The purpose of this section is to learn the must-knows about complex numbers to be able to move-on to more advanced theorems and techniques for polynomials. In particular, the Fundamental Theorem of Algebra (FTA) and the Complex Conjugate Zeros Theorem.

Definition: Imaginary Numbers

An imaginary number is any number that can be written: \[a.i\] Where:

  • \(a \in \mathbb{R}\), \(a\) can be any real number
  • \(i = \sqrt{-1}\).

Since \(i = \sqrt{-1}\) an immediate and important result is that: \[i^2 = -1\] So, for instance, given the two imaginary numbers \(3i\) and \(4i\), we can calculate their product as follows: \[\begin{aligned} 3i \times 4i & = 3\times 4 \times i^2 \\ & = 12 \times (-1) \\ 3i \times 4i & = -12 \end{aligned}\]

Definition: Complex Numbers

A complex number is made of two parts:

  • a Real Part
  • an Imaginary Part
We often refer to complex numbers with the variable \(z\) and write: \[z = a + ib\] Where \(a\) and \(b\) are both real numbers and are the respective real and imaginary parts of the complex number \(z\) and \(i\) is \(i = \sqrt{-1}\).

Example

Each of the following are complex numbers:

  • The number defined as: \[z = 2 + 3i\] is a complex number. Its real part is \(2\), its imaginary part is \(3\).
  • The number defined as: \[z = 3 - 5i\] is a complex number. Its real part is \(3\), its imaginary part is \(-5\).
  • The number defined as: \[z = 6i\] is a complex numbers. Its real part is \(0\), its imaginary part is \(6\).
  • The number defined as: \[z = -7\] is a complex numbers. Its real part is \(-7\), its imaginary part is \(0\).

Notation

Given a complex number, \(z = a+ib\), to refer to its real and imaginary parts, \(a\) and \(b\), we write:

  • \(Re(z) = a\)
  • \(Im(z) = b\)

Example

Consider the complex number \(z = 2 + 4i\). This number has real and imaginary: \[Re(z) = 2 \quad Im(z) = 4\]

Graphical Representation of Complex Numbers : Argand Diagram

Given a complex number \(z = a+ ib\), we can represent it on the Argand diagram, also called the complex plane, which works in the same way as an \(xy\) grid.

The Argand diagram consists of:

  • a Real axis, which is the horizontal axis
  • an Imaginary axis, which is the vertical axis
So a complex number \(z=a+ib\) is represented by a point with coordinates \(\begin{pmatrix}a,b\end{pmatrix}\), where:
  • \(a\) is the amount we move along the real axis
  • \(b\) is the amount we move along the imaginary axis.

Example

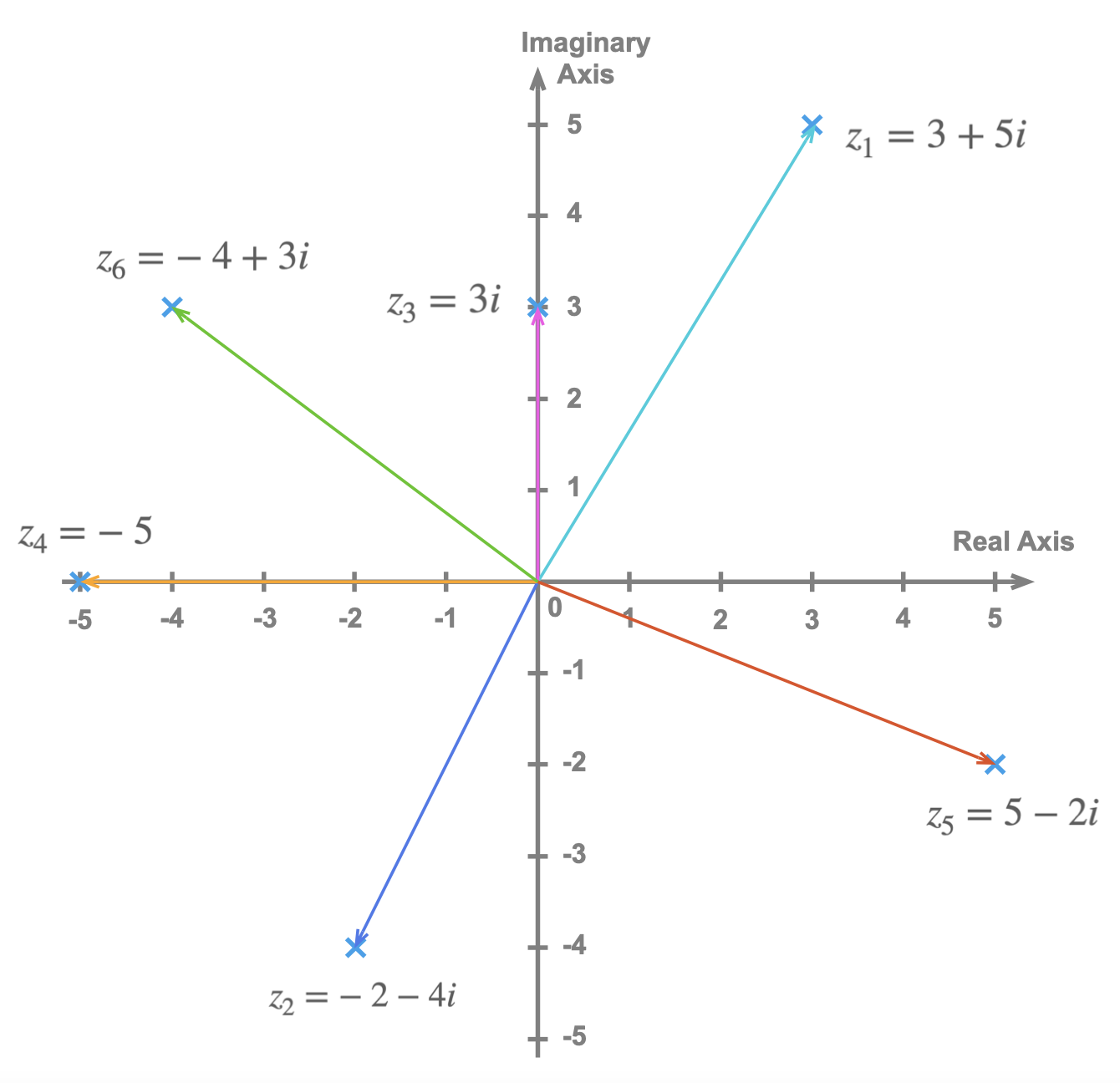
Plot each of the following complex numbers on an Argand diagram:

  • \(z_1 = 3 + 5i\)
  • \(z_2 = -2-4i\)
  • \(z_3 = 3i\)
  • \(z_4 = -5\)
  • \(z_5 = 5-2i\)
  • \(z_6 = -4+3i\)

Solution

Each of the complex numbers:

  • \(z_1 = 3 + 5i\)
  • \(z_2 = -2-4i\)
  • \(z_3 = 3i\)
  • \(z_4 = -5\)
  • \(z_5 = 5-2i\)
  • \(z_6 = -4+3i\)
is plotted on the Argand diagram, shown here.

Notice that \(z_3=3i\) is on the vertical imaginary axis and is known as a pure imaginary. Also, \(z_4=-5\) is on the real axis; it is a real number represented in the complex plane. This highlights the fact that the set of real numbers is a proper subset of the set of complex numbers: \[\mathbb{R} \subset \mathbb{C}\]

Addition/Subtraction with Complex Numbers

Given two complex numbers, \(z_1 = a+ib\) and \(z_2 = c + id\), we add/subtract by adding/subtracting their respective real and imaginary parts: \[\begin{aligned} z_1 \pm z_2 & = \begin{pmatrix} a + ib \end{pmatrix} \pm \begin{pmatrix} c + id \end{pmatrix} \\ & = a + ib \pm c \pm id \\ z_1 \pm z_2 & = \begin{pmatrix} a \pm c \end{pmatrix} + i \begin{pmatrix} b \pm d \end{pmatrix} \end{aligned}\]

Tutorial: Adding & Subtracting Complex Numbers

In this tutorial we learn the rule for adding and subtracting with complex numbers and work through the following example:

Given \(z_1 = 2+3i\), \(z_2 = 6+4i\), \(z_3=5i\) and \(z_4 = 7\), find:

  1. \(z_1 + z_2\)
  2. \(z_1 - z_2\)
  3. \(z_2 + z_3\)
  4. \(z_4 - z_1\)

Example 1

Given the two complex numbers \(z_1 = 2+3i\) and \(z_2 = 3 - 5i\) we can add them as follows: \[\begin{aligned} z_1 + z_2 & = \underbrace{2+3i}_{z_1} + \underbrace{3-5i}_{z_2} \\ & = \underbrace{2+3}_{\text{real parts together}} + \underbrace{3i-5i}_{\text{imaginary parts together}} \\ z_1 + z_2 & = 5 - 2i \end{aligned}\]

Example 2

Given the two complex numbers \(z_1 = 8+5i\) and \(z_2 = 3 + 2i\) we can subtract \(z_2\) from \(z_1\) as follows: \[\begin{aligned} z_1 - z_2 & = \underbrace{8+5i}_{z_1} - \underbrace{3+2i}_{z_2} \\ & = \underbrace{8-3}_{\text{real parts}} + \underbrace{5i-2i}_{\text{imaginary parts}} \\ z_1 - z_2 & = 5 + 3i \end{aligned}\]

Multiplication by a Scalar

Given a complex number \(z = a+ib\) we can multiply it by a scalar \(k \in \mathbb{R}\) as follows: \[\begin{aligned} k.z & = k\begin{pmatrix} a + ib \end{pmatrix} \\ & = k.a + ik.b \end{aligned}\] put "simply" we multiply both the real and the imaginary part by the number \(k\).

Tutorial: Multiplying a Complex Number by a Scalar (a Real Number)

In this tutorial we learn the rule for complex numbers by scalars and work through the following example:

Given \(z = 2+3i\), find:

  1. \(4z\)
  2. \(-5z\)

Example 3

Given the complex number \(z = 3 + 4i\) we can find \(5z\) as follows: \[\begin{aligned} 5z & = 5\begin{pmatrix} 3 + 4i\end{pmatrix}\\ & = 5\times 3 + 5\times 4i \\ & = 15 + 20i \end{aligned}\]

Complex Conjugates

Given a complex number \(z = a+ib\), we define its complex conjugate

, typically written \(z^*\), as: \[z^* = a - ib\] We say that two complex numbers are complex conjugates of each other if they have the same real part and opposite imaginary parts.

On the Argand diagram, complex conjugates are the reflections of each other across the real axis.

Example

Given the complex number \(z = 3+2i\), find its complex conjugate and plot both \(z\) and (z^*\) on the Argand diagram.

Solution

The complex conjugate of \(z = 3+2i\) has opposite imaginary part. It is therefore: \[z^* = 3 - 2i\] Important: on the Argand diagram a complex number \(z\) and its complex conjugate \(z^*\) will always be reflections of each other across the Real axis.

This is illustrated, for this example, on the Argand diagram we see here.

Addition & Subtraction with Conjugates

Given a complex number \(z = a + ib\) and its conjugate \(z^* = a - ib\), their sum and difference leads to the following results:

  • addition \(z+z^*\): \[z + z^* = 2.Re(z)\]
  • subtraction \(z-z^*\): \[z - z^* = 2i.Im(z)\]

Example

Given \(z = 3 + 5i\) and its complex conjugate \(z^* = 3 - 5i\):

  • \(z + z^* = 2\times 3 = 6\)
  • \(z - z^* = 2i \times 5 = 10i\)

Exercise 1

For each of the following questions, express your answer in its simplest form:

  1. Find \(z_1+z_2\) where \(z_1 = 4 + i\) and \(z_2 = -2 + 3i\).
  2. Find \(z_1 - z_2\) where \(z_1 = 6 + 3i\) and \(z_2 = 4 + i\).
  3. Find \(5z\) where \(z = -3 + 5i\).
  4. Find \(4z_1 + 2z_2\) where \(z_1 = 1 + 4i\) and \(z_2 = 3 - i\).
  5. Find \(z_1 + z^*_1 - z_2\) where \(z_1 = -4 + 2i\) and \(z_2 = -6i\)
  6. Find \(z_1 - 3z_2\) where \(z_1 = 3-2i\) and \(z_2 = 1+ 5i\).
  7. Find \(z_2 + \begin{pmatrix} z_1 - z^*_1 \end{pmatrix}\), where \(z_1 = 3 + 2i\) and \(z_2 = 4 + 5i\).
  8. Find \(4z_1 + 3z_2 - 2z_3\) where \(z_1 = -2 + i\), \(z_2 = 3 + 4i\) and \(z_3 = 4\).
  9. Find \(z_1 + z_2 +z^*_1 - z^*_2\) where \(z_1 = 1 - 3i\) and \(z_2 = 6 +i\).
  10. Find \(5z_1 - 4z_2 + z_3\) where \(z_1 = 3+4i\), \(z_2 = 1 - 3i\) and \(z_3 = 4 + 2i\).

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 1

Solution Without Working

Multiplying Two, or more, Complex Numbers

Given two complex numers \(z_1 = a+ib\) and \(z_2 = c + id\), we find the product: \[z_1 . z_2 = \begin{pmatrix}a + ib \end{pmatrix}.\begin{pmatrix}c + id \end{pmatrix}\] using the "usual" rules of distributivity, keeping in mind that \(i^2 = -1\).

Example 4

Given the two complex numbers \(z_1 = 4+5i\) and \(z_2 = 3 + 2i\) we multiply these two complex numbers together as follows: \[\begin{aligned} z_1.z_2 & = \begin{pmatrix} 4 + 5i \end{pmatrix}.\begin{pmatrix} 3 + 2i \end{pmatrix} \\ & = 4\times 3 + 4\times 2i + 5i \times 3 + 5i \times 2i \\ & = 12 + 8i + 15i + 10i^2 \\ & = 12 + 8i + 15i - 10 \\ z_1.z_2 & = 2 + 23i \end{aligned}\]

Tutorial: Multiplying a Complex Numbers Together

In this tutorial we learn the how to multiply complex numbers together. We work through the following example:

Given \(z_1 = 3 - 2i\), \(z_2 = 4 + i\) and \(z_3 = 6i\), find:

  1. \(z_1.z_2\)
  2. \(z_2.z_3\)

Important Result: Product of Complex Conjugates

Given a complex number \(z = a+ib\) and its complex conjugate \(z^* = a - ib\), their product will always equal to the sum of the squares of the real and the imaginary part of \(z\): \[z.z^* = a^2+b^2\]

Proof

This result can be shown as follows: \[\begin{aligned} z.z^* & = \begin{pmatrix}a + ib \end{pmatrix}.\begin{pmatrix} a - ib \end{pmatrix} \\ & = a^2 - iab + iab - b^2i^2 \\ z.z^* & = a^2 + b^2 \end{aligned}\]

Example

Given \(z = 2 + 5i\) and its conjugate \(z^* = 2 - 5i\), their product is: \[\begin{aligned} z.z^* &= \begin{pmatrix} 2+5i \end{pmatrix}.\begin{pmatrix} 2-5i \end{pmatrix} \\ & = 2^2 + 5^2 \\ z.z^* & = 29 \end{aligned}\]

Exercise 2

For each of the following questions, express your answer in its simplest form:

  1. Expand and simplify: \(\begin{pmatrix}1 + 3i \end{pmatrix}.\begin{pmatrix}5 + 2i \end{pmatrix}\)
  2. Expand and simplify: \(\begin{pmatrix}3 - 4i \end{pmatrix}.\begin{pmatrix}2 + 6i \end{pmatrix}\)
  3. Given \(z_1 = 3 - 4i\) and \(z_2 = 1 + 5i\), find: \[2.z_2 - z_1.z^*_1\]
  4. Expand and simplify: \(\begin{pmatrix}2 - i \end{pmatrix}.\begin{pmatrix}6 - 3i \end{pmatrix}\)
  5. Given \(z_1 = 3i\) and \(z_2 = 7+i\), find: \[3.z_1.z^*_1 + z_2.z^*_2\]
  6. Expand and simplify: \(\begin{pmatrix}5 + 3i \end{pmatrix}.\begin{pmatrix}7 + i \end{pmatrix}\)
  7. Given \(z_1 = 5 +2i\) and \(z_2 = 1+i\), find: \[4.z_1 \begin{pmatrix}z^*_1 - z_2 \end{pmatrix}\]
  8. Expand and simplify: \(\begin{pmatrix}-2 + 5i \end{pmatrix}.\begin{pmatrix}3 - 2i \end{pmatrix}\)
  9. Given \(z_1 = -4 +i\) and \(z_2 = 6 + 7i\), find: \[\begin{pmatrix}z_1+z_2\end{pmatrix}.\begin{pmatrix}z^*_1 - z^*_2 \end{pmatrix}\]
  10. Find \(2z_1 + z_2.z_3\), where \(z_1 = 1+2i\), \(z_2 = 2 + 4i\) and \(z_3 = 3 - i\).
  11. Find \(z_1.z_2 - 4z_3\), where \(z_1 = 2 + i\), \(z_2 = 3 - i\) and \(z_3 = 3 + 2i\).
  12. Find \(3z_1.z_2 - 2z_3\), where \(z_1 = 5 + 2i\), \(z_2 = 2 - 3i\) and \(z_3 = 6 + 4i\).

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 2

Division with Complex Numbers

Given two complex numbers \(z_1 = a + ib\) and \(z_2 = c + id\), we can divide \(z_1\) by \(z_2\) using the complex conjugate of \(z_2\). Given \(z_2 = c + id\) its complex conjugate is \(z^*_2 = c - id\). Using the fact that \(z_2 \times z^*_2 = c^2 + d^2\), we can divide \(z_1\) by \(z_2\) as explained in the following tutorial.

Tutorial: Division with Complex Numbers

In this tutorial we learn the how to divide one complex number by another. We work through the following examples:

  1. \(\frac{3 - 4i}{1+2i}\)
  2. \( \frac{3+i}{-2i}\)

Example

Given \(z_1 = 8 -2i\) and \(z_2 = 2 + 5i\) we find \(z_1 \div z_2\) as follows: \[\begin{aligned} z_1 \div z_2 & = \frac{z_1}{z_2} \\ & = \frac{8 - 2i}{2 + 5i} \\ & = \frac{8 - 2i}{2 + 5i} \times \frac{2 - 5i}{2 - 5i} \\ & = \frac{\begin{pmatrix} 8 - 2i \end{pmatrix}. \begin{pmatrix} 2 - 5i \end{pmatrix}}{\begin{pmatrix} 2 + 5i \end{pmatrix}. \begin{pmatrix} 2 - 5i \end{pmatrix}} \\ & = \frac{16 - 40i - 4i +10i^2}{4 + 25} \\ & = \frac{16 - 44i -10}{29} \\ & = \frac{6 - 44i}{29}\\ z_1 \div z_2 & = \frac{6}{29} - \frac{44}{29}i \end{aligned}\]

Exercise 3

  1. Given \(z_1 = 3+4i\) and \(z_2 = 1+2i\), find:
    1. \(z_1 \div z_2\)
    2. \(z_2 \div z_1\)
  2. Given \(z_3 = -2 + 3i\) and \(z_4 = 5+i\), find:
    1. \(z_3 \div z_4\)
    2. \(z_4 \div z_3\)
  3. Given \(z_5 = 6 - 2i\) and \(z_6 = 8i\), find:
    1. \(z_5 \div z_6\)
    2. \(z_6 \div z_5\)
  4. Given \(z_1 = 1 + 3i\), \(z_2 = 4-i\) and \(z_3 = 5 + 7i\), find: \[z_1+z_2 \div z_3\]
  5. Given \(z_1 = 5-3i\), \(z_2 = 4i\) and \(z_3 = 1 + 2i\), find: \[3z_1 - \frac{z_2}{2z_3}\]

Note: this exercise can be downloaded as a worksheet to practice with: Worksheet 3

Modulus of a Complex Number

Given a complex number, \(z=a+ib\), it's modulus, written \(\begin{vmatrix}z\end{vmatrix}\), equals to the distance from \(z\) to the origin of the Argand diagram. \[\begin{vmatrix}z\end{vmatrix} = \sqrt{a^2+b^2}\]

Example

Find the modulus of the complex number: \[z = 3+4i\]

Solution

Using the formula, stated above: \[\begin{aligned} \begin{vmatrix}z\end{vmatrix} & = \sqrt{3^2+4^2} \\ & = \sqrt{9+16} \\ & = \sqrt{25} \\ \begin{vmatrix}z\end{vmatrix} & = 5 \end{aligned}\]

Distance Between 2 Complex Numbers

Given two complex numbers \(z_1 = a+ib\) and \(z_2 = c+id\) we can calculate the distance, \(D\), between them using: \[D = \begin{vmatrix} z_2 - z_1\end{vmatrix} \quad \text{or} \quad D = \begin{vmatrix} z_1 - z_2\end{vmatrix}\] Focusing on \(D = \begin{vmatrix} z_2 - z_1\end{vmatrix}\) leads to the following formula in terms of \(a\), \(b\), \(c\) and \(d\): \[\begin{aligned} D &= \begin{vmatrix} z_2 - z_1\end{vmatrix} \\ & = \begin{vmatrix} \begin{pmatrix}c+id\end{pmatrix} - \begin{pmatrix}a + ib \end{pmatrix} \end{vmatrix} \\ & = \begin{vmatrix} \begin{pmatrix}c-a\end{pmatrix} + i\begin{pmatrix}d - b\end{pmatrix} \end{vmatrix} \\ D & = \sqrt{\begin{pmatrix}c-a\end{pmatrix}^2 + \begin{pmatrix}d - b\end{pmatrix}^2} \end{aligned}\]

Example

Find the distance between the two complex numbers \(z_1 = -1 + i\) and \(z_2 = 2+5i\).

Solution

Using the formula stated above, we can calculate the distance \(D\) as follows: \[\begin{aligned} D & = \begin{vmatrix}z_2 - z_1 \end{vmatrix} \\ & = \begin{vmatrix} \begin{pmatrix}2+5i\end{pmatrix} - \begin{pmatrix}-1+i\end{pmatrix} \end{vmatrix} \\ & = \begin{vmatrix} 2+5i + 1-i \end{vmatrix} \\ & = \begin{vmatrix} 3+4i \end{vmatrix} \\ & = \sqrt{3^2 + 4^2} \\ & = \sqrt{25} \\ D & = 5 \end{aligned}\]

Creating Sets with the Modulus

The modulus is often used to create sets on the Argand Diagram (sets in the Complex Plane). Since \(\begin{vmatrix}z\end{vmatrix}\) equals to the distance from \(z\) to the origin we can create sets of the type: \[A = \left \{ z \in \mathbb{C} | \begin{vmatrix} z \end{vmatrix} \leq k \right \} \quad \text{or} \quad B = \left \{ z \in \mathbb{C} | \begin{vmatrix} z \end{vmatrix} < k \right \}\] Where:

  • set \(A\) refers to all of the complex numbers, in the Complex Plane, whose distance from the origin is less than or equal to some value \(k\)
  • set \(B\) refers to all of the complex numbers, in the Complex Plane, whose distance from the origin is less than to some value \(k\)

Here are some examples:

Example 1

We can refer to all the complex numbers on the Argand diagram whose distance is less than, or equal to, 3 units from the origin with the set \(A\) defined as: \[A = \left \{ z \in \mathbb{C} | \begin{vmatrix} z \end{vmatrix} \leq 3 \right \}\] This set is illustrated here, with the disc of radius \(3\) centered at the origin.

Example 2

We can refer to all the complex numbers on the Argand diagram whose distance is less than 2 units from the origin with the set \(B\) defined as: \[B = \left \{ z \in \mathbb{C} | \begin{vmatrix} z \end{vmatrix} < 2 \right \}\] This set is illustrated here, with the disc of radius \(2\) centered at the origin.

Notice the circumference is dotted to highlight the fact that the distance from the origin must be less than 2 and can't equal to 2.

Example 3

We can refer to all the complex numbers on the Argand diagram whose distance is less than, or equal to, 2 units from 3 on the real axis with the set \(C\) defined as: \[C = \left \{ z \in \mathbb{C} | \begin{vmatrix} z - 3 \end{vmatrix} \leq 2 \right \}\] This set is illustrated here, with the disc of radius \(2\) centered at 3 on the real axis.

Example 4

We can refer to all the complex numbers on the Argand diagram whose distances are less than 3 units from the complex number \(-3+2i\) with the set \(D\) defined as: \[D = \left \{ z \in \mathbb{C} | \begin{vmatrix} z - (-3+2i) \end{vmatrix} < 3 \right \}\] This set is illustrated here, with the disc, whose circumference is dotted, of radius \(3\) centered at \(-3+2i\).


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.