Polynomials - Factor & Remainder Theorem
(Factoring Polynomials)
In this section we learn about the factor and remainder theorems. These theorems are at the heart of factoring polynomials and finding a polynomial's roots (or zeros).
We state each theorem as well as see how they can be used with tutorials. We also work through some exam type questions, which can be downloaded as pdf worksheets.
Remainder Theorem
Given a polynomial function, \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0\), the remainder, upon division by a linear function, \(g(x) = x - c\), is equal to \(f(c)\).
What this means (and enables us to do)
The remainder theorem provides us with a quick and efficient way of calculating the remainder when a polynomial is being divided by a linear of the type \(g(x) = x-c\).
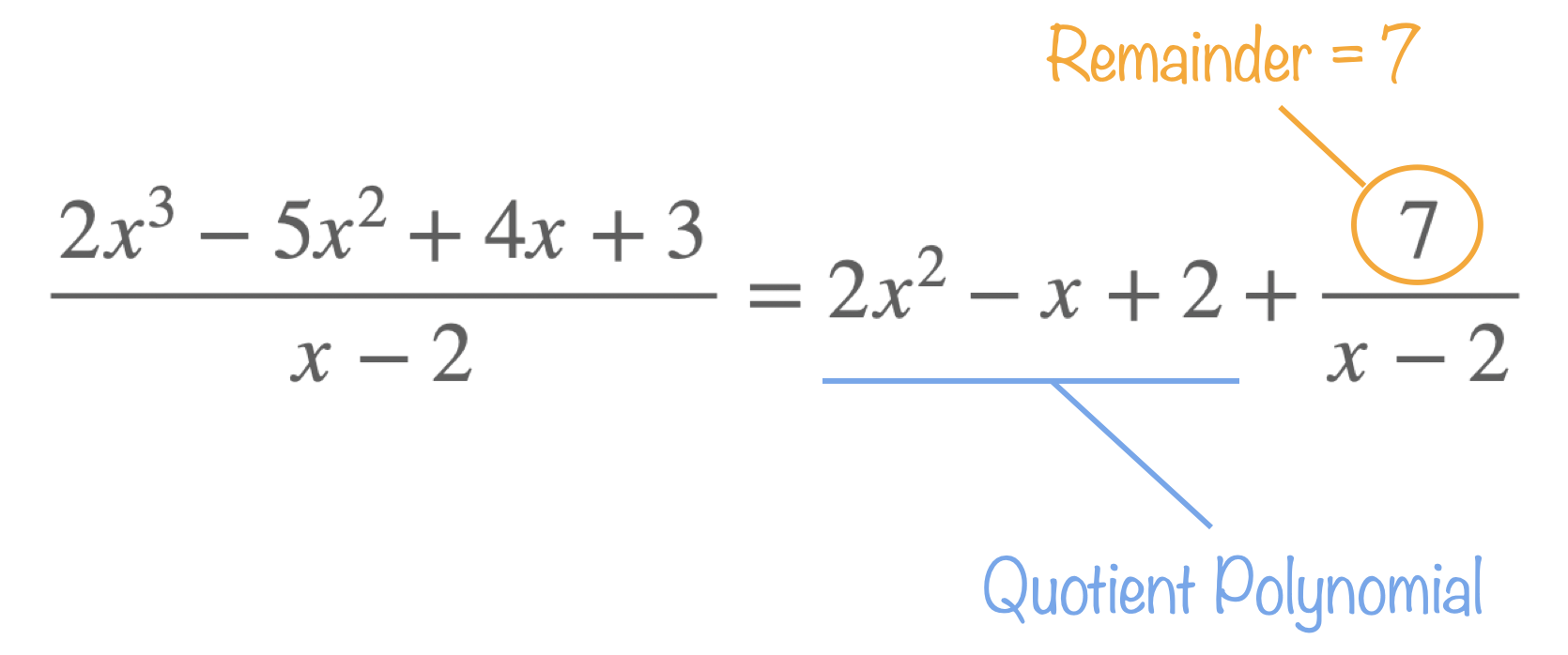 For instance, say we're dividing \(f(x)=2x^3 - 5x^2 + 4x + 3\) by \(g(x) = x-2\), then the remainder theorem allows us to quickly state that the remainder of this division is \(f(2)=7\).
For instance, say we're dividing \(f(x)=2x^3 - 5x^2 + 4x + 3\) by \(g(x) = x-2\), then the remainder theorem allows us to quickly state that the remainder of this division is \(f(2)=7\).
Indeed:
\[\begin{aligned} f(2) & = 2\times 2^3 - 5\times 2^2 + 4 \times 2 + 3 \\
& = 16 - 20 + 8 + 3 \\
f(2) & = 7 \end{aligned}\]
In the following tutorial we illustrate the remainder theorem further and show how Horner's Algorthm, or synthetic division, quickly enables us to find both:
- the remainder
- the quotient polynomial
Tutorial: Remainder Theorem for Polynomials
In this tutorial, we learn how to use the remainder theorem to find the remainder obtained when dividing a polynomial by a linear. In doing so, we also see how to actually divide a polynomial by a linear using Horner's Method for evaluating polynomials.
Remainder Theorem Exam Question
In the following tutorial I work through a must-know exam question invovling the remainder there:
\(f(x)\) is defined as: \[f(x) = 2x^3 + px^2 - 10x - 11\] Given the remainder upon division by \(x-3\) is \(58\), find the value of \(p\).
Tutorial: Remainder Theorem Exam Question with Unknown Coefficient
Exercise 1 - Remainder Theorem
- Find the remainder obtained when dividing \(f(x) = 3x^3 - 4x^2 + x - 2\) by \(\begin{pmatrix}x-3\end{pmatrix}\).
- Find the remainder obtained when dividing \(f(x) = 3x^5 - x^3 + 4x^2 + x + 19\) by \(x+1\).
- Given when we divide \(f(x) = 2x^3 - 7x^2 + px + 3\) by \(\begin{pmatrix}x - 2 \end{pmatrix}\) the remainder is \(-9\), find the value of \(p\).
- The function \(f(x) = -3x^3 + px^2 + 5x + 10\) leaves a remainder of \(94\) when divided by \(\begin{pmatrix} x + 3\end{pmatrix}\)
- \(f(x) = -x^3 + cx^2 + x + 18\). Find what \(c\) has to be for the remainder, upon division by \(x-5\), to be \(-52\).
Factor Theorem for Polynomials
Given a polynomial function, \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0\), and a number \(c\) (real or complex) the factor theorem states that:
Factor & Remainder Theorems go "hand in hand"
The factor theorem tells provides with two tools:
- if we're told that \(f(c) = 0\) then we can state (without further proof) that \(\begin{pmatrix}x - c\end{pmatrix}\) is a factor of \(f(x)\)
- if we're told that \(\begin{pmatrix}x - c\end{pmatrix}\) is a factor of \(f(x)\), then we can state (without further proof) that \(f(c) = 0\).
In essence, the factor theorem is "just" a special case of the remainder theorem.
Indeed, with the remainder theorem in mind, when the remainder \(R\) of \(\frac{f(x)}{x-c}\) equals to zero, \(f(c)=R=0\), then \(\begin{pmatrix}x-c\end{pmatrix}\) is, by very definition, a factor of \(f(x)\).
Furthermore since the remainder theorem tells us:
It's Just Like with Whole Numbers
Note: in the same way that \(4\) isn't a factor of \(13\) because: \[13 \div 4 = 3 \ R \ 1\] but \(4\) is a factor of \(12\) because: \[12 \div 4 = 3 \ R \ 0\] if the remainder upon division by \(\begin{pmatrix} x - c \end{pmatrix}\) isn't equal to \(0\) then \(\begin{pmatrix} x - c \end{pmatrix}\) isn't a factor and \(f(c) \neq 0\): \[\frac{f(x)}{x-c} = Q(x) + \frac{R}{x-c} \quad , \ R \neq 0\] if the remainder upon division by \(\begin{pmatrix} x - c \end{pmatrix}\) equals \(0\) then \(\begin{pmatrix} x - c \end{pmatrix}\) is a factor and \(f(c) = 0\): \[\frac{f(x)}{x-c} = Q(x)\]
Factoring Polynomials
The factor theorem provides us with a method for factoring polynomials. Indeed, if we know that a number \(c\) is a zero (or root) of a polynomial \(f(x)\), that is if: \[f(c) = 0\] then the factor theorem tells us that \(\begin{pmatrix}x - c \end{pmatrix}\) is factor of \(f(x)\). This means that there must be a quotient function, \(Q(x)\), such that: \[f(x) = \begin{pmatrix}x - c \end{pmatrix}.Q(x)\] The quotient function, \(Q(x)\), is a polynomial function whose degree is \(1\) less than the degree of \(f(x)\): \[\text{Deg}\begin{bmatrix} Q(x)\end{bmatrix} = \text{Deg}\begin{bmatrix} f(x)\end{bmatrix} - 1\] to find what the quotient polynomial is we use synthetic division of polynomials.
Step-by-Step Worked Example
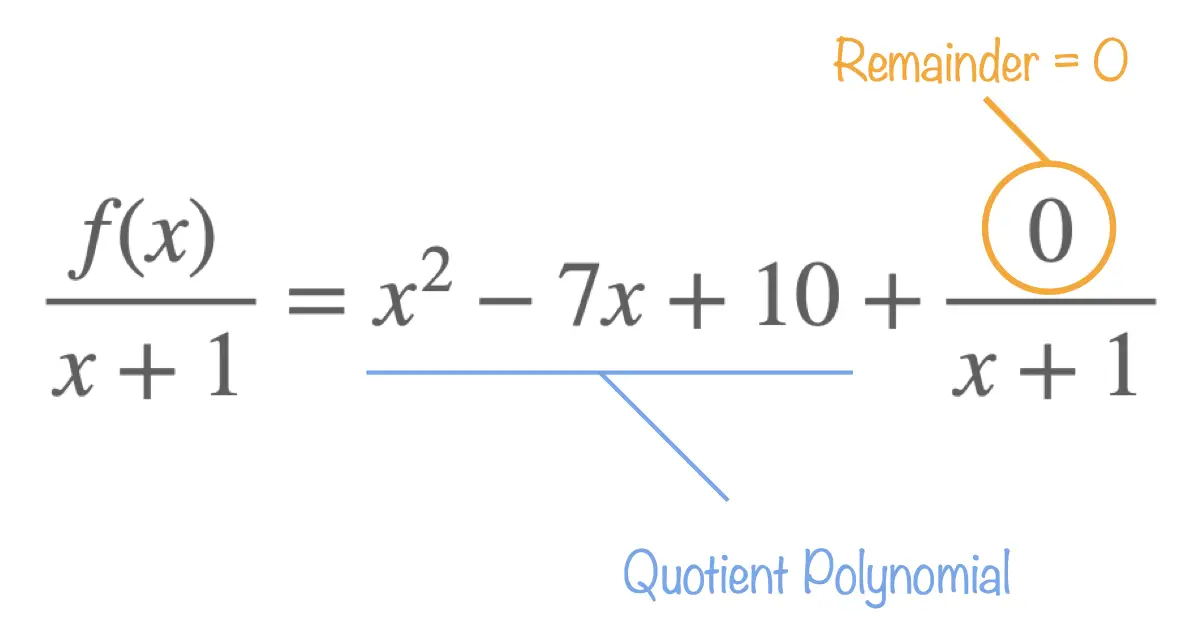 Multiplying both sides of:
\[\frac{f(x)}{x+1} = x^2 - 7x + 10 + \frac{0}{x+1}\]
by \(\begin{pmatrix} x+1 \end{pmatrix}\)
leads to:
\[f(x) = \begin{pmatrix}x+1\end{pmatrix}\begin{pmatrix}x^2 - 7x + 10 \end{pmatrix}\]
which highlights the fact that \(\begin{pmatrix}x+1\end{pmatrix}\) is a factor of \(f(x)\).
Multiplying both sides of:
\[\frac{f(x)}{x+1} = x^2 - 7x + 10 + \frac{0}{x+1}\]
by \(\begin{pmatrix} x+1 \end{pmatrix}\)
leads to:
\[f(x) = \begin{pmatrix}x+1\end{pmatrix}\begin{pmatrix}x^2 - 7x + 10 \end{pmatrix}\]
which highlights the fact that \(\begin{pmatrix}x+1\end{pmatrix}\) is a factor of \(f(x)\).
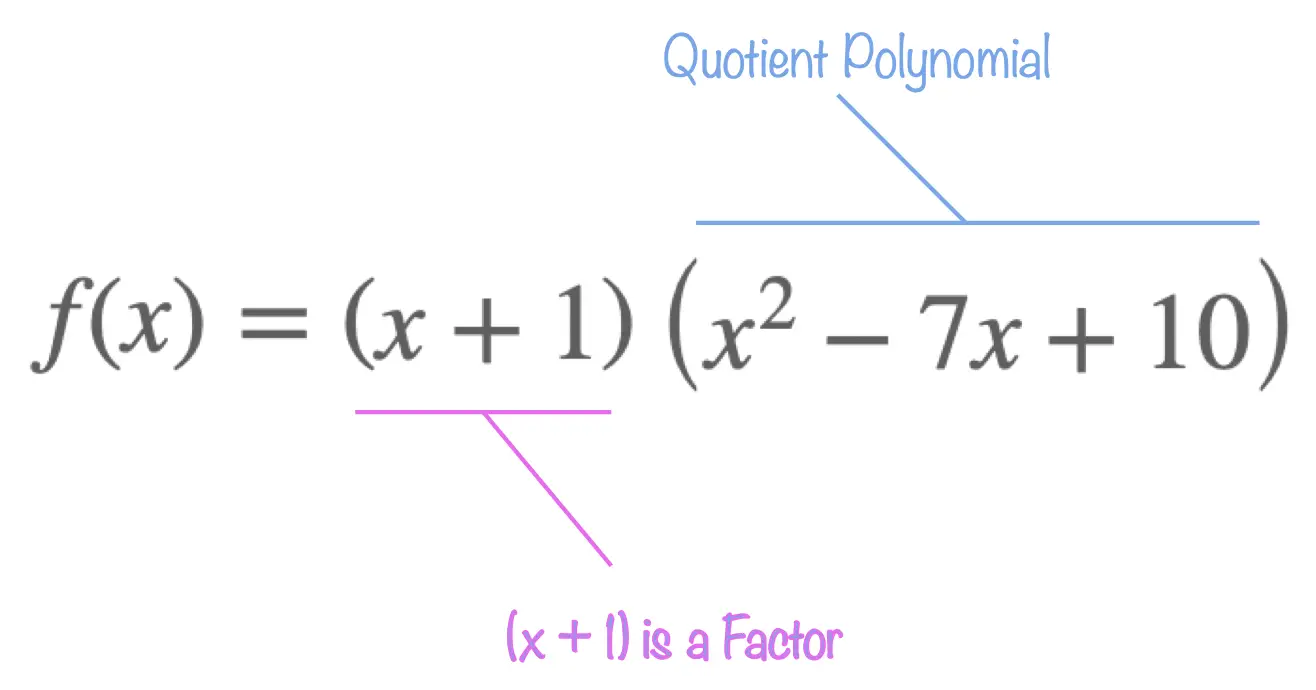 Multiplying both sides of:
\[\frac{f(x)}{x+1} = x^2 - 7x + 10 + \frac{0}{x+1}\]
by \(\begin{pmatrix} x+1 \end{pmatrix}\)
leads to:
\[f(x) = \begin{pmatrix}x+1\end{pmatrix}\begin{pmatrix}x^2 - 7x + 10 \end{pmatrix}\]
which highlights the fact that \(\begin{pmatrix}x+1\end{pmatrix}\) is a factor of \(f(x)\).
Multiplying both sides of:
\[\frac{f(x)}{x+1} = x^2 - 7x + 10 + \frac{0}{x+1}\]
by \(\begin{pmatrix} x+1 \end{pmatrix}\)
leads to:
\[f(x) = \begin{pmatrix}x+1\end{pmatrix}\begin{pmatrix}x^2 - 7x + 10 \end{pmatrix}\]
which highlights the fact that \(\begin{pmatrix}x+1\end{pmatrix}\) is a factor of \(f(x)\).
Since \(Q(x)\) is also a polynomial function, provided we can find its zeros, we can factor it as well. Repeatedly factoring the quotient polynomial we get we can potentially write a polynomial of degree \(n\): \[f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0\] in factored form, as a product of upto \(n\) linear factors: \[f(x) = a_n \begin{pmatrix}x - c_1 \end{pmatrix}\begin{pmatrix}x - c_2 \end{pmatrix} \dots \begin{pmatrix}x - c_n \end{pmatrix}\] The following couple of tutorials show examples of how the factor theorem, as well as synthetic division can be used to write a cubic polynomial in factored form.
Factoring Polynomials
Since the quotient function \(Q(x)\) is also a polynomial function we can look for its zeros and therefore its factors. Say \(x=c_2\) is one of the zeros of \(Q(x)\) then we can write: \[Q(x) = \begin{pmatrix}x-x_2\end{pmatrix}Q_2(x)\] Going back to \(f(x)\), and letting \(c = c_1\) and \(Q(x) = Q_1(x)\) we can therefore write: \[f(x) = \begin{pmatrix}x-c_2 \end{pmatrix}\underbrace{\begin{pmatrix}x - c_1 \end{pmatrix} Q_2(x)}_{Q_1(x)}\] By repeatedly doing this, a polynomial of degree \(n\), \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x +a_0\), can be written as a product of upto \(n\) linear factors, \(x-c_1\), \(x-c_1\), ... , \(x-c_n\) in \(\mathbb{R}\).
Note: when working within the set of complex numbers \(\mathbb{C}\), a polynomial of degree \(n\) will always have \(n\) zeros and therefore \(n\) linear factors \(x-c_1\), \(x-c_1\), ... , \(x-c_n\): \[f(x)=a_nx^n+a_{n-1}x^{n-1} + \dots + a_1x + a_0 = a_n \begin{pmatrix}x-c_n\end{pmatrix}\begin{pmatrix}x-c_{n-1}\end{pmatrix} \dots \begin{pmatrix}x-c_2\end{pmatrix}\begin{pmatrix}x-c_1\end{pmatrix}\]
Exercise 2
Using the factor theorem answer each of the following:
- Show that \(\begin{pmatrix}x+1 \end{pmatrix}\) is a factor of \(f(x) = 2x^4 - x^3 - 2x^2 - 4x - 5\).
- Is \(\begin{pmatrix}x - 2 \end{pmatrix}\) a factor of \(f(x) = 3x^3 - 5x^2 + 4x - 12\)? Justify your answer.
- Is \(\begin{pmatrix}x + 3 \end{pmatrix}\) a factor of \(f(x) = -x^3 + x^2 + 11x - 1\)? Justify your answer.
- \(f(x) = 2x^3 + 3x^2 + cx + 5\). Find what \(c\) has to be for \(x+5\) to be a factor.
- Given \(\begin{pmatrix}x-2\end{pmatrix}\) is a factor of \(f(x) = x^3 - 5x^2 + px - 10\), find the value of \(p\).
Exam Questions with 2 unknown Coefficients
The following tutorials show
Tutorial: Remainder Theorem 2 Unknown Coefficients
In this tutorial, we learn how to use the remainder theorem to find the remainder obtained when dividing a polynomial by a linear. In doing so, we also see how to actually divide a polynomial by a linear using Horner's Method for evaluating polynomials.
Tutorial: Factor & Remainder Theorem 2 Unknown Coefficients
In this tutorial, we learn how to use the remainder theorem to find the remainder obtained when dividing a polynomial by a linear. In doing so, we also see how to actually divide a polynomial by a linear using Horner's Method for evaluating polynomials.
Exercise 3
- Given \(x-5\) is a factor of \(f(x) = 2x^3 + px^2 + qx - 15\) and that \(f(x)\) leaves a remainder of \(-33\) when divided by \(\begin{pmatrix}x-2\end{pmatrix}\). Find \(p\) and \(q\).
-
Consider the function \(f(x) = x^3 + px^2 + qx + 8\) :
- the remainder when we divide by \(x+1\) is \(14\)
- the remainder when we divide by \(x-3\) is \(74\)
-
The polynomial \(f(x) = px^4 + 4x^3 + qx^2 - 28x - 48\) is such that:
- \(x-2\) is a factor of \(f(x)\)
- \(x+3\) is a factor of \(f(x)\)
- The function \(f(x) = x^4 - 18x^2 + px + q\) has a factor \(x+5\) and leaves a remainder of \(8\) when divided by \(x-3\). Find \(p\) and \(q\).
Solution Without Working
- \(p = -10 \quad q = 30\)
- \(p = 5 \quad q = -2\)
- \(p = -2 \quad q = 26\)
- \(p = 33 \quad q = -10\)
Scan this QR-Code with your phone/tablet and view this page on your preferred device.
 Subscribe to Our Channel
Subscribe to Our Channel
Subscribe Now and view all of our playlists & tutorials.