RadfordMathematics.com

Pythagoras' Theorem and its Converse Theorem

Pythagoras' Theorem, also called Pythagorean Theorem, is perhaps one of the most well-known theorems in mathematics.

Given a right-angled triangle, for which two of the sides lengths are known : Pythagoras' theorem provides us with a formula for calculating the length of the remaining (third) side length.

The converse of this theorem, on the other hand, provides us with a tool for checking whether or not a given triangle is right-angled or not.

Pythagoras' Theorem

If a triangle is a right-angle triangle then the square of its hypotenuse is equal to the sum of the squares of its other two sides.

Note: by definition, the hypotenuse is the side length opposite the right angle.

\[c^2 = a^2+b^2\]

Worked Example 1

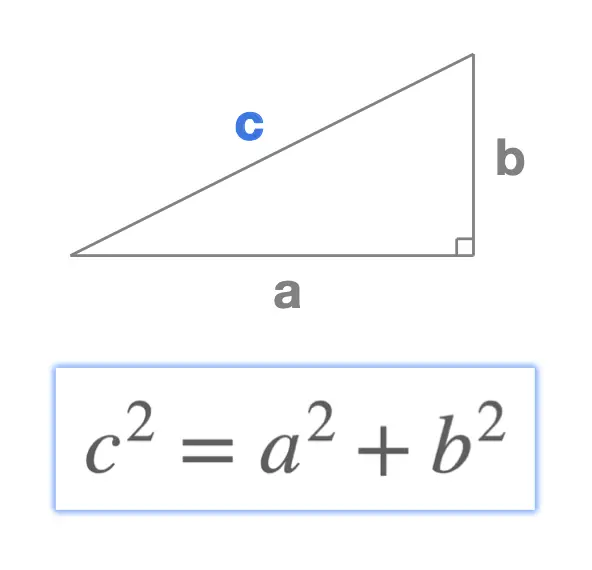
Consider the right angled triangle shown here. What is the length of the side marked \(x\) ?

Solution

Since this is a right-angle triangle, we can use Pythagoras' theorem to find the unknown side length.

Using the formula for the theorem: \[c^2 = a^2+b^2\] where \(c\) is the hypotenuse (side length opposite the right angle), we replace \(a\) by \(8\), \(b\) by \(6\) and \(c\) by \(x\), which leads to: \[x^2 = 8^2+6^2\] Now that we've written the formula, we solve this equation for \(x\): \[\begin{aligned} x^2 & = 8^2+6^2 \\ x^2 & = 64 + 36 \\ x^2 &= 100 \end{aligned}\] Now that we know that \(x^2= 100\) all we need to do is take the square root of each side: \[\begin{aligned} x & = \sqrt{100}\\ x & = 10 \end{aligned}\]

Worked Example 2

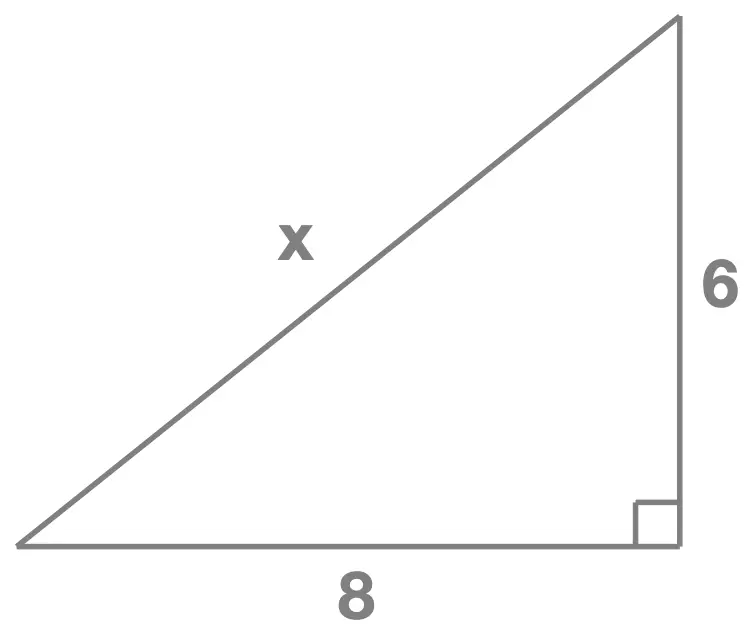
Consider the right angled triangle shown here. What is the length of the side marked \(x\) ?

Solution

Since this is a right-angle triangle, we can use Pythagoras' theorem to find the unknown side length. Notice that in this example the unknown side length isn't the hypotenuse but one of the other two sides.

Using the formula for the theorem: \[c^2 = a^2+b^2\] where \(c\) is the hypotenuse (side length opposite the right angle), we replace \(a\) by \(5\), \(b\) by \(x\) and \(c\) by \(12\), which leads to: \[12^2 = 5^2+x^2\] Calculating \(12^2\) and \(5^2\) this becomes: \[144 = 25 + x^2\] We now isolate the \(x^2\) by subtracting 25 from both sides: \[119 = x^2\] which we can re-write as: \[x^2 = 119\] taking the square root of each side: \[x = \sqrt{119}\]

Finally using our calculator to calculate \(\sqrt{119}\): \[\begin{aligned} x & = \sqrt{119} \\ x & = 10.9087 \\ x & = 10.9 \quad \text{(rounded to 1dp)} \end{aligned}\]

Now that we've seen the formula as well as a couple of worked examples, it's worth watching this video in which I work through 3 examples.

In each case I use Pythagoras' Theorem to find an unknown side in a right angled triangle.

Tutorial: Pythagoras' Theorem

In the following tutorial we learn how to use Pythagoras' Theorem for finding an unknown side. Several examples are worked through.

Converse Theorem

Given 3 sides of a triangle, the Converse of Pythagoras' Theorem allows us to determine whether or not it is a right-angled triangle.

Converse Theorem

Given a triangle, if the square of the longest side is equal to the sum of the squares of the other two sides then it is a right-angled triangle and the longest side is its hypotenuse.

Tutorial: Converse Theorem

In the following tutorial we learn how to use Pythagoras' Theorem for finding an unknown side. Several examples are worked through.

Worked Example 3

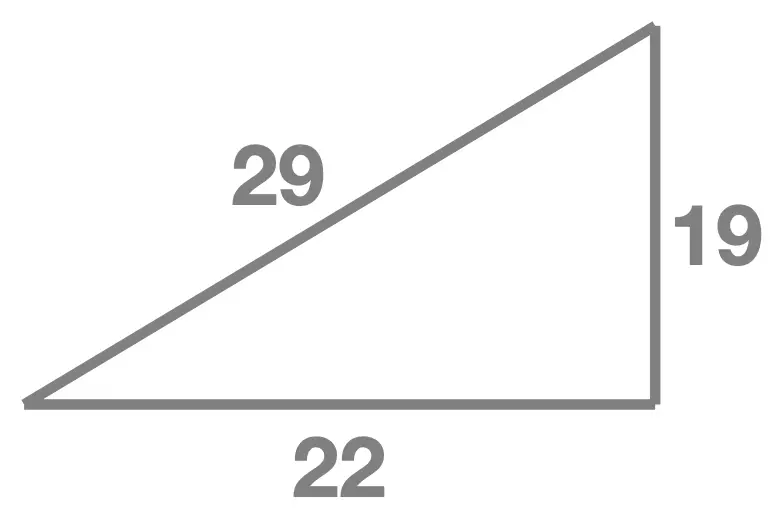Consider the triangle shown here. Is it a right-angled triangle ?

Solution

Since we know all three sides of the triangle, we can use the converse theorem to determine whether or not it is right angled.

We make a note of:

  • the longest side : \(29\)
  • the other two sides : \(19\) and \(22\)
We now calculate:
  • the square of the longest side : \(29^2 = 841\)
  • the sum of the squares of the other two sides: \[\begin{aligned} 19^2 + 22^2 & = 361 + 484 \\ & = 845 \end{aligned}\]
Finally we compare the results obtained and conclude: \[841 \neq 845\] Since \(841 \neq 845\) : the square of the longest side length isn't equal to the sum of the squares of the other two sides and we can conclude that : this triangle is not a right-angled triangle and it doesn't have a hypotenuse.

Worked Example 4

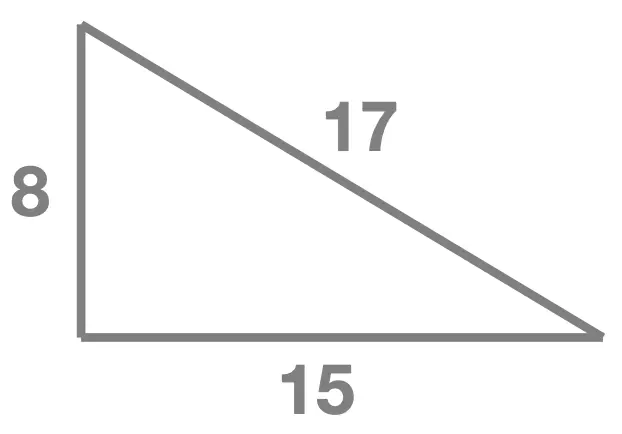Consider the triangle shown here. Is it a right-angled triangle ?

Solution

Just as in example 3, since we know all three sides of this triangle, we can use the converse theorem to determine whether or not it is right angled.

We make a note of:

  • the longest side : \(17\)
  • the other two sides : \(8\) and \(15\)
We now calculate:
  • the square of the longest side : \(17^2 = 289\)
  • the sum of the squares of the other two sides: \[\begin{aligned} 8^2 + 15^2 & = 64 + 225 \\ & = 289 \end{aligned}\]

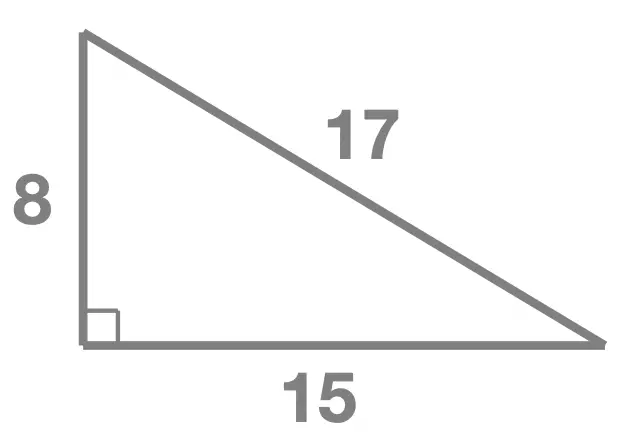Finally we compare the results obtained and conclude: \[289 = 289\] Since \(289 = 289\) (the two results obtained are equal) : the square of the longest side length is equal to the sum of the squares of the other two sides and we can conclude that : this triangle is a right-angled triangle and it has a hypotenuse equal to \(17\), which is (by definition) the side opposite the right angle.

Exam Style Questions

The following questions are typical exam-style questions students may be faced with in an exam.

Exam Question 1

Starting from town A, Sarah cycles West for 13km to reach town B. She then cycles South for 14km to reach town C. Finally Sarah cycles straight from town C to town A.

Find the distance cycled from C to A.

Solution

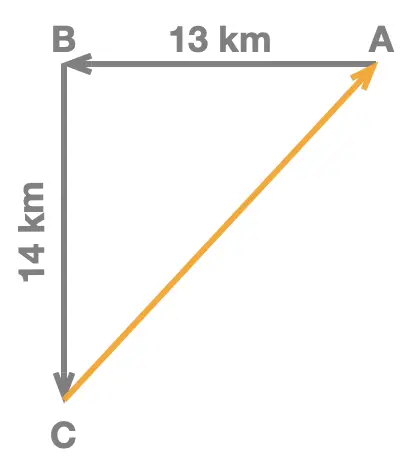We start by drawing Sarah's route, which we've done on the right hand side of the screen.

We quickly realize that the triangle ABC is a right angle triangle, whose \(90^{\circ}\) angle is at B (since the EAST-WEST and NORTH-SOUTH directions are perpendicular to each other).

Consequently we can use Pythagoras' Theorem to find the length AC, which is the triangle's hypotenuse. We can write: \[AC^2 = AB^2 + BC^2\] Replacing AB and BC by their respective values this becomes: \[\begin{aligned} AC^2 & = 13^2 + 14^2 \\ & = 169 + 196 \\ & = 365 \end{aligned}\]

Finally applying the square root to both sides : \[\begin{aligned} AC & = \sqrt{365} \\ & = 19.105 \\ AC & = 19.1 \quad \text{(rounding to 3 significant figures)} \end{aligned}\] The direct route from C to A is 19.1km long.

Exam Question 2

Consider the right angle triangle shown here:

Find the value of \(x\).

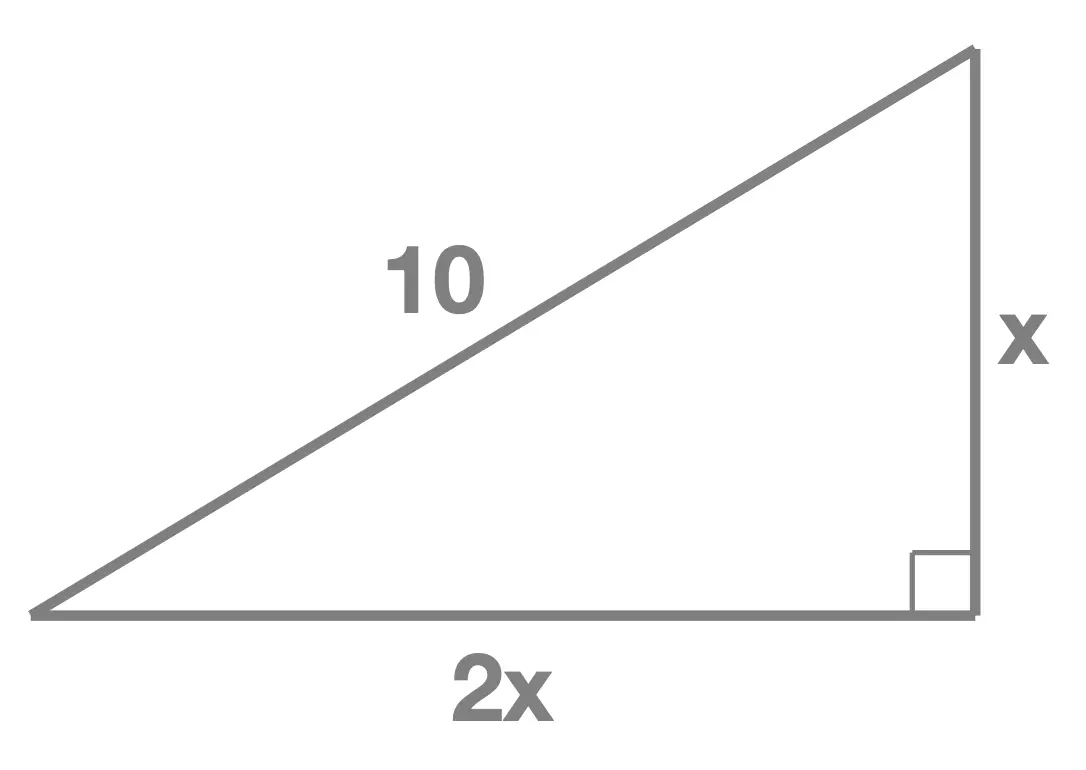
Solution

Since this is a right angle triangle, whose hypotenuse is \(10\), we can use Pythagoras' theorem to write: \[10^2 = x^2 + \begin{pmatrix}2x\end{pmatrix}^2\] We now take care of the powers of 2 and seek to solve for \(x\).

Note: careful to remember \(\begin{pmatrix}ab\end{pmatrix}^n = a^nb^n\) so \(\begin{pmatrix}2x\end{pmatrix}^2 = 2^2x^2\).

\[\begin{aligned} & 10^2 = x^2 + \begin{pmatrix}2x\end{pmatrix}^2 \\ & 100 = x^2 + 2^2x^2 \\ & 100 = x^2 + 4x^2 \\ & 100 = 5x^2 \end{aligned}\] Dividing both sides by \(5\): \[\begin{aligned} & \frac{100}{5} = x^2 \\ & 20 = x^2 \end{aligned}\] We can write this with \(x^2\) on the left hand side: \[x^2 = 20 \] Applying the square root to both sides: \[\begin{aligned} x & = \sqrt{20} \\ & = 4.47214 \\ x & = 4.47 \quad \text{(rounded to 3 significant figures)} \end{aligned}\] Finally we can state that \(x = \sqrt{20}\) (exact value) or that \(x=4.47\) when rounded to 3 significant figures.


Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.