Fundamental Theorem of Algebra (FTA)
(Writing Polynomials in Root-Factored Form)
We now learn about the Fundamental Theorem of Algebra (FTA), which, alongside its corollary and the factor theorem, will allow us to solve any polynomial equation as well as root factor any polynomial.
Fundamental Theorem of Algebra (FTA)
Given a polynomial function \(f(x)\), with real or complex coefficients: \[f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x+a_0\] The fundamental theorem of algebra states:
Another, and perhaps simpler, way of thinking of the fundamental theorem of algebra (FTA) is that when working within \(\mathbb{C}\) (the set of complex numbers) an equation of the form: \[a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x+a_0 = 0\] will always have at least one solution.
Careful, if we're "only" working within \(\mathbb{R}\) (the set of real numbers) the FTA is no longer true. Indeed, if we're working within the set or real numbers, there is no rule in \(\mathbb{R}\) that says that a polynomial equation must have a solution. An example of this is quickly shown with the following equation: \[x^2+4 = 0\] in \(\mathbb{R}\) this equation has no solution, which illustrates the fact that in \(\mathbb{R}\) the FTA isn't true. On the other hand, if we're working in \(\mathbb{C}\) it has two solutions: \(x = -2i\) and \(x = 2i\).
Corollary 1 of the FTA
Since there must exist a value \(x=c_1\) such that: \[f(c_1)=0\] The factor theorem allows us to state:
Given a polynomial function of degree \(n\): \[f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x+a_0\] there is at least one value of \(x\), say \(x = c_1\) such that: \[f(x) = \begin{pmatrix}x - c_1 \end{pmatrix}.Q_1(x)\] where \(Q_1(x)\) is the quotient polynomial function of degree \(n-1\) obtained by dividing \(f(x)\) by \(\begin{pmatrix}x-c_1 \end{pmatrix}\) : \[Q_1 (x) = \frac{f(x)}{x-c_1}\]
Root Factoring Polynomials
As we've just seen, the polynomial \(f(x)\) can be written \(f(x) = \begin{pmatrix}x - c_1 \end{pmatrix}.Q_1(x)\). But since \(Q_1(x)\) is itself a polynomial function we can apply the FTA to it and state that there is a value \(x\), say \(x = c_2\), such that: \[Q_1(c_2)=0\] and once more we can use the corrolary of the FTA, this time to state that: \[Q_1(x) = \begin{pmatrix}x - c_2 \end{pmatrix}.Q_2(x)\] and therefore, going back to \(f(x)\), we can write: \[f(x) = \begin{pmatrix}x - c_1 \end{pmatrix}.Q_1(x) = \begin{pmatrix}x - c_1 \end{pmatrix}.\begin{pmatrix}x - c_1\end{pmatrix}.Q_2(x) \] Following the same "pattern" \(n\) times, for \(Q_2(x)\), \(Q_3(x)\), ... \(Q_n(x)\) leads to writing the polynomial function in its root factored form: \[f(x) = a_n\begin{pmatrix}x - c_1\end{pmatrix}.\begin{pmatrix}x - c_2\end{pmatrix}. \dots . \begin{pmatrix}x - c_n\end{pmatrix}\] Where : \[a_n = Q_n(x)\] The idea behind root factoring polynomials is written more formally in corollary 2.
Corallary 2: Root Factoring Polynomials
Any a polynomial function: \[f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x+a_0\] can be written as a product of its n linear factors: \[f(x) = a_n\begin{pmatrix}x - c_1\end{pmatrix}.\begin{pmatrix}x - c_2\end{pmatrix}. \dots . \begin{pmatrix}x - c_n\end{pmatrix}\] Where: \[f(c_1) = f(c_2) = \dots = f(c_n) = 0\] This also means that \(f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x + a_0\) has \(n\) roots (\(n\) zeros).
What this means
This corallary is it is telling us that a polynomial of degree \(n\) can be written as a product of \(n\) linear factors. This also means that the polynomial has \(n\) zeros (roots).
Careful: this is true so long as we are accepting roots to be complex numbers, in \(\mathbb{C}\). If we're working exclusively with real numbers then the fundamental theorem of algebra tells us that a polynomial function of degree \(n\): \[f(x) = a_nx^n + a_{n-1}x^{n-1} + \dots + a_1x+a_0\] can have upto \(n\) real roots.
Example 1
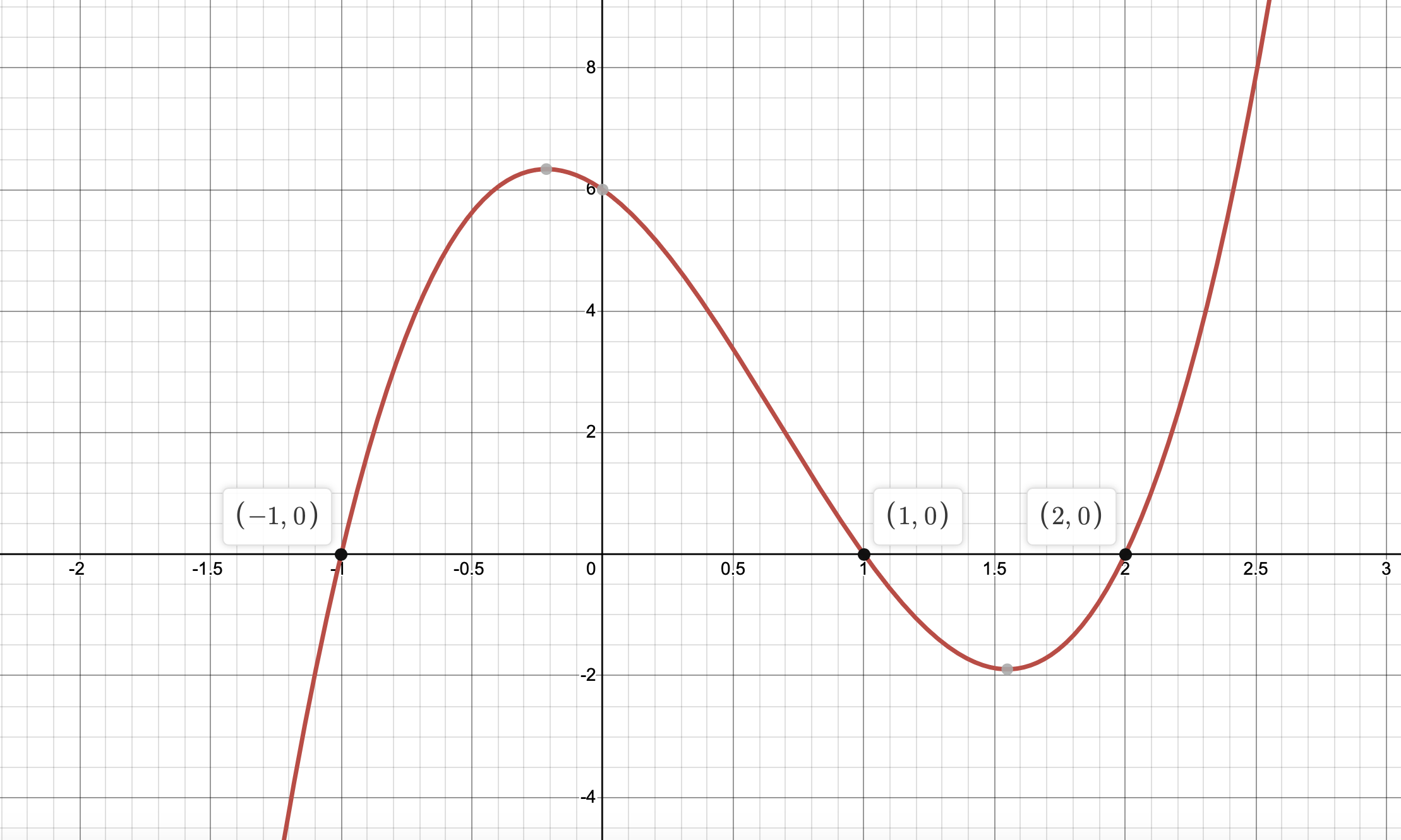 The polynomial function:
\[f(x)= 3x^3 - 6x^2 - 3x + 6\]
Has \(3\) real roots:
\[\left \{-1, \ 1, \ 2 \right \}\]
In other words:
\[f(-1)=f(1)=f(2) = 0\]
And we can write this polynomial in its root factored form as:
\[f(x) = 3.\begin{pmatrix}x+1\end{pmatrix}.\begin{pmatrix}x-1\end{pmatrix}.\begin{pmatrix}x-2\end{pmatrix}\]
The polynomial function:
\[f(x)= 3x^3 - 6x^2 - 3x + 6\]
Has \(3\) real roots:
\[\left \{-1, \ 1, \ 2 \right \}\]
In other words:
\[f(-1)=f(1)=f(2) = 0\]
And we can write this polynomial in its root factored form as:
\[f(x) = 3.\begin{pmatrix}x+1\end{pmatrix}.\begin{pmatrix}x-1\end{pmatrix}.\begin{pmatrix}x-2\end{pmatrix}\]
Example 2
The polynomial function: \[f(x) = 2x^5 - 12x^4 + 30x^3 - 60x^2 + 88x - 48\] has \(3\) real roots and \(2\) complex roots: \[\left \{1, \ 2, \ 3, \ -2i, \ 2i \right \}\] in other words: \[f(1)=f(2)=f(3) = f(-2i) = f(2i)= 0\] In its root factored form, this polynomial can therefore be written: \[f(x) = 2.\begin{pmatrix}x-1\end{pmatrix}.\begin{pmatrix}x-2\end{pmatrix}.\begin{pmatrix}x-3\end{pmatrix}.\begin{pmatrix}x-2i\end{pmatrix}.\begin{pmatrix}x+2i\end{pmatrix}\]
In both of the examples, above, the polynomials has distinct roots; the cubic has \(3\) distinct roots and the quintic polynomial had \(5\) distinct roots. That won't always be the case.
Example
For instance the cubic polynomial: \[f(x) = x^3 - 3x^2 + 3x - 1\] has three identical roots at \(x = 1\). In root-factored form we can write: \[f(x) = \begin{pmatrix}x - 1\end{pmatrix}.\begin{pmatrix}x - 1\end{pmatrix}.\begin{pmatrix}x - 1\end{pmatrix}\] Or "simply": \[f(x) = \begin{pmatrix}x - 1\end{pmatrix}^3\] We say that the root has multiplicity of \(3\).
Multiplicity of Roots
Given a polynomial, with a root, or zero, \(c\) such that \(f(c) = 0\). \(c\) is said to have multiplicity \(m\) if, in root factored form, \(f(x)\) has \(m\) linear factors equal to \(\begin{pmatrix}x-c \end{pmatrix}\).
Consequently, a root's multiplicity is the power to which we can raise the linear factor, when writing \(f(x)\) in its factored form: \[\begin{pmatrix}x - c \end{pmatrix}^m\]
Example 3 : Cubic Polynomial
In root factored form, the polynomial \(f(x) = x^3 + x^2 - 5x + 3\), is written: \[f(x) = \begin{pmatrix}x + 3\end{pmatrix}. \begin{pmatrix}x - 1 \end{pmatrix}^2\] we say that the root \(x = 1\) has multiplicity \(2\).
Below, we can see how to reach this result by hand.
Solution

Example 4 : Quintic (degree 5) Polynomial
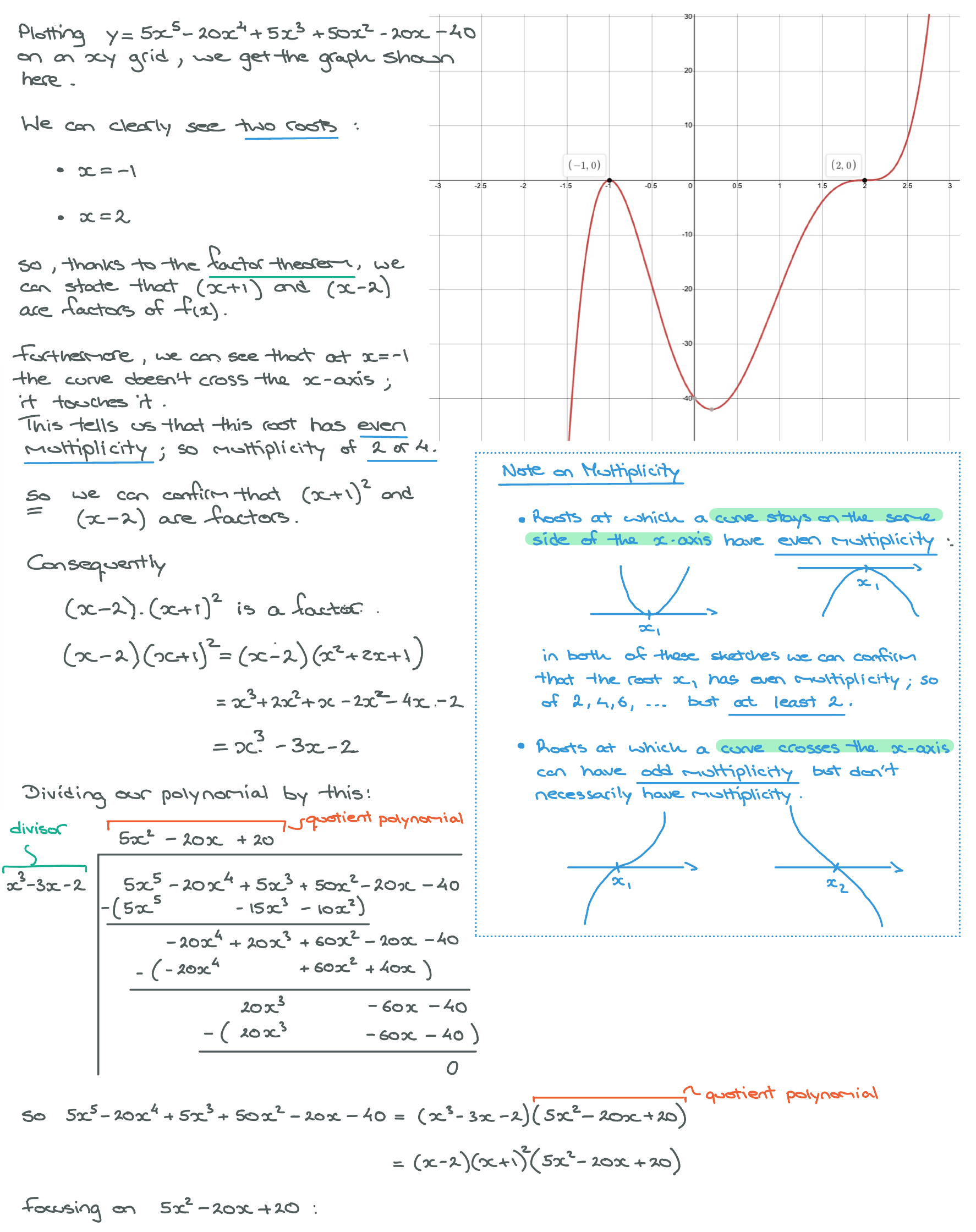
The polynomial \(f(x) = 5x^5 - 20x^4 + 5x^3 + 50x^2 - 20x - 40\) can be written in factored form as: \[f(x) = 5.\begin{pmatrix} x+1\end{pmatrix}^2.\begin{pmatrix} x - 2 \end{pmatrix}^3\] The root \(x = -1\) has multiplicity of \(2\) and the root \(x = 2\) has multiplicity of \(3\).
Below, we can see how to reach this result by hand alongside our graphical calculator.
Solution

Scan this QR-Code with your phone/tablet and view this page on your preferred device.

Subscribe Now and view all of our playlists & tutorials.