Introduction to Probabilities

(Terminology, Definitions, Venn Diagrams & Probability of a Single Event)

Probabilities are the study of "chance". When we calculate the probability of something occurring we are calculating the likelihood of it happening.

Studying probabilities will allow us to answer questions like:

What is the probability of rolling an even number with a dice?
What is the probability of winning the lottery?
What is the probability of picking two red balls from a bag with 4 red balls and 6 green balls?
What is the probability that it will rain in Ireland on Febrary 14th?

Before learning how to answer such questions we need to learn some terminology related to probabilities, this is necessary to know how to express ourselves in this topic.

Definition of a Probability

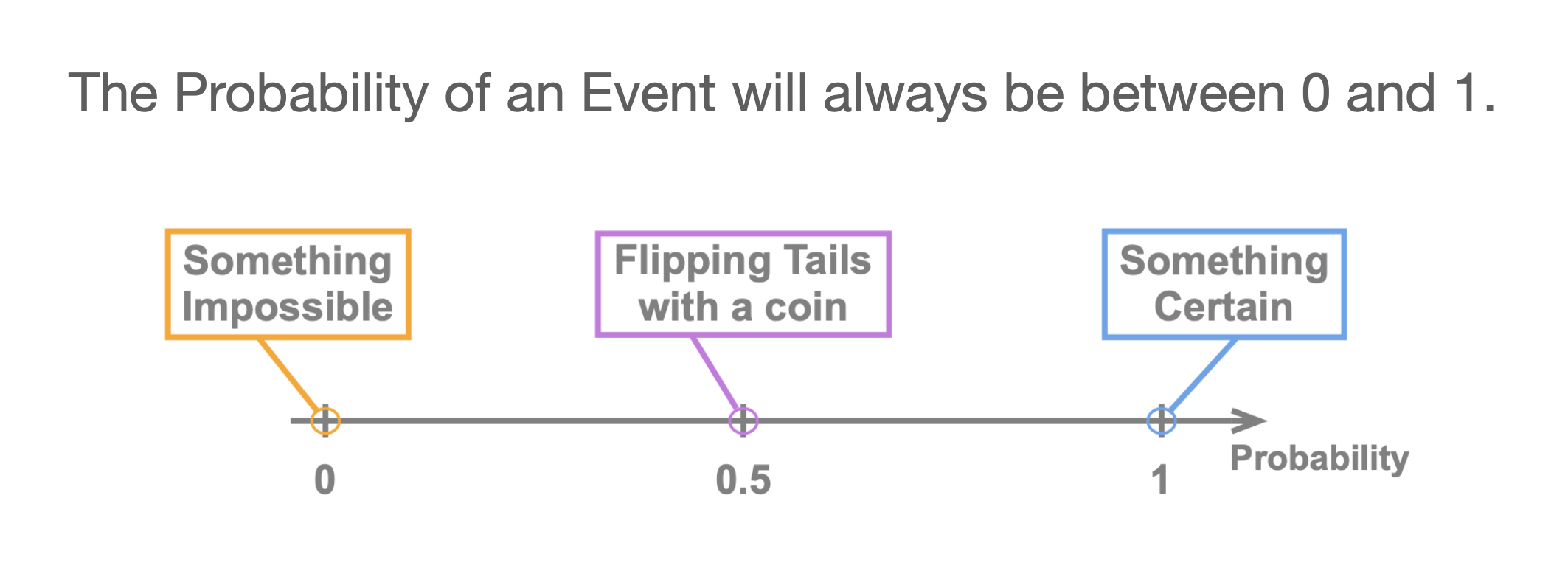
A probability is a measure of the likeliness of an event, which depends on chance, occurring. All probabilities are measured on a scale from \(0\) to \(1\), where:

An event whose probability is \(0\) is an impossible event (something that cannot happen).
An event whose probability os \(1\) is an event that is certain to occur.

All other events have a probability that lies somewhere between those two values.

Here are some examples of probabilities:

The probability of flipping Tails with an unbiased coin is \(p\begin{pmatrix}\text{Heads}\end{pmatrix} = \frac{1}{2} = 0.5\).
The probability of rolling a \(6\) with a single die is \(p\begin{pmatrix}\text{Six}\end{pmatrix} = \frac{1}{6} \approx 0.17\).
The probability of flipping tails twice in a row with an unbiased coin is \(p\begin{pmatrix}\text{2 Tails in a Row}\end{pmatrix} = \frac{1}{4} = 0.25\).

Experiments & Outcomes

In probabilities, an experiment is a process (could be "anything") in which there are one or more (usually more) possible outcomes each of which depends on chance.

EXAMPLES

The following table lists some experiments with their corresponding outcomes:

EXPERIMENT	OUTCOMES
Flipping an unbiaed (a fair) coin.	There are 2 possible outcomes: Heads or Tails.
Rolling a six faced die and making a note of the result.	The possible outcomes are: \(1\), \(2\), \(3\), \(4\), \(5\) or \(6\).
Picking a marble, at random, from a bag containing \(3\) orange marbles and \(4\) green marbles.	The possible outcomes are: picking an orange marble or picking a green marble.

Events in Probability

Given an experiment, an event refers to either:

one specific outcome
a combination of several outcomes

We'll usually refer to events using a capital letter, \(A\), \(B\), \(C\), ... .

EXAMPLES

Here are a few examples of experiments, their outcomes, and some of the events we may be interested in:

EXPERIMENT	OUTCOMES	EVENTS
Flipping an unbiaed (a fair) coin.	There are 2 possible outcomes: Heads or Tails.	We could define the events: \(H\): flipping Heads \(T\): flipping Tailes
Rolling a six faced die and making a note of the result.	The possible outcomes are: \(1\), \(2\), \(3\), \(4\), \(5\) or \(6\).	We could define the events: \(A\): rolling an even number \(B\): rolling a number greater than 4 \(C\): rolling a number that is both an even number and greater than 4
Picking a marble, at random, from a bag containing \(3\) orange marbles and \(4\) green marbles.	The possible outcomes are: picking an orange marble or picking a green marble.	We could define the two events: \(G\): picking a Green marble \(B\): picking a Blue marble

Sample Space

Given an experiment, the sample space tells us, or shows us, all of the possible outcomes. The possible outcomes are often written in between curly braces \( \{ \text{outcome 1, outcome 2,} \cdots \} \).

Examples

When we flip a coin there are two distinct possible outcomes, Heads (H) and Tails (T). In this case we could say that the sample space is: \[U = \{H,\ T \}\] Note: we'll often call the sample space \(S\) or \(U\) (to refer to the Universal Set, defined with Venn diagrams further down).

When we roll a singke die and look at the number we obtained, there are \(6\) possible outcomes: \(1\), \(2\), \(3\), \(4\), \(5\) and \(6\). We can state that the sample space is: \[U = \{1, \ 2, \ 3, \ 4, \ 5, \ 6 \}\]

Venn Diagrams (for Probabilities)

Given an experiment, we'll often use a Venn diagram to illustrate:

all of the possible outcomes
the events we're interested in.

As such a Venn diagram provides with a nice way to quickly picture the Sample Space as well as determine how many outcomes correspond to a given event.

Example

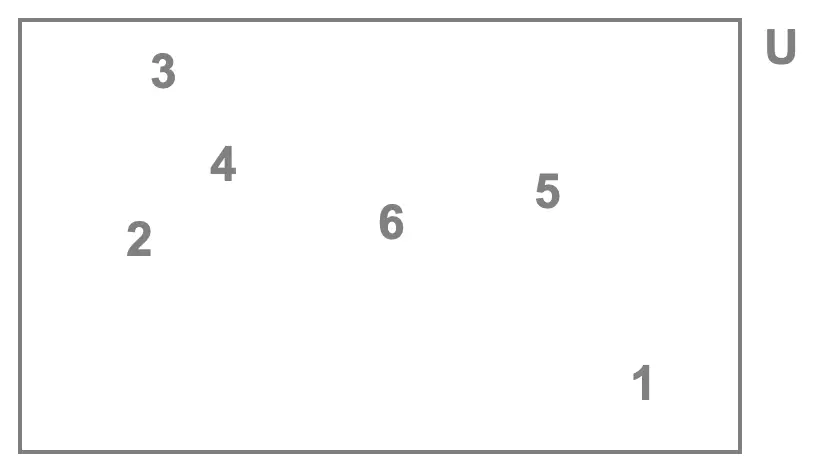
Say we're rolling a single die and looking at the number obtained and that we're interested in the events:

\(A\): rolling an even number
\(B\): rolling a number greater than \(3\).

We can summarize the experiment as well as those two events with Venn Diagrams like the two shown here:

Venn Diagram 1

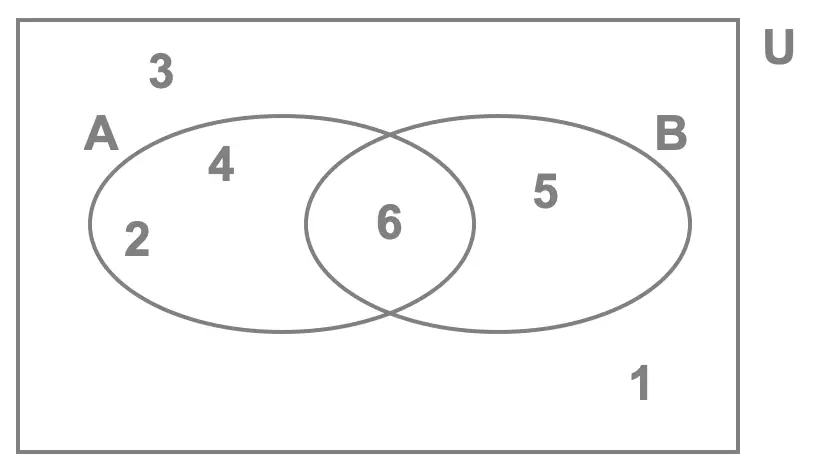
This first Venn diagram shows the Sample Space, represented by the universal set, \(U\). We can see all of the possible outcomes of the experiment (rolling a die) are listed inside \(U\).

Venn Diagram 2

In this second Venn diagram we've grouped the elements correspoding to each of the two events \(A\) and \(B\). When working with Venn diagrams we call these groups of elements "sets". So each event is represented by a set.

Number of Ways an Event Can Occur = Number of Elements in a Set

As we're about to see, further down, when calculating the probability of an event ocurring we'll need to find the number of ways that event can occur in the experiment.

If we're using a Venn diagram, then the number of ways an event \(A\) can occur is equal to the number of elements in set \(A\) on the Venn diagram.

Looking back at the Venn diagram we created, above, and the two events:

\(A\): rolling an even number
\(B\): rolling a number greater than \(4\).

we can see that there are:

\(3\) elements inside set \(A\), we write \(n\begin{pmatrix}A \end{pmatrix} = 3\), so the number of ways event \(A\) can occur is \(3\)
\(2\) elements inside set \(B\), we write \(n\begin{pmatrix}B \end{pmatrix} = 2\), so the number of ways event \(B\) can occur is \(2\)

Note: this Venn diagram also shows us the total number of possible outcomes. Indeed counting all of the elements in the set we can see that the total number of possible outcomes is \(6\), that's the total number of elements in the set \(U\), so we can write \(n\begin{pmatrix}U\end{pmatrix}=6\).

Probability of a Single Event

Given an experiment as well as an event \(A\), we calculate the probability of event \(A\) occurring with the formule: \[p\begin{pmatrix}A\end{pmatrix} = \frac{n \begin{pmatrix}A \end{pmatrix}}{n\begin{pmatrix}U\end{pmatrix}}\] where:

\(n\begin{pmatrix}A\end{pmatrix}\) refers to the numbers of ways event \(A\) can occur. On a Venn Diagram that equals to the number of elements inside set \(A\).
\(n\begin{pmatrix}U\end{pmatrix}\) refers to the total number of possible outcomes in the experiment. On a Venn Diagram that equals to the total number of elements inside set \(U\).

Example

Clara rolls un unbiased die and looks at the number she rolls.

Find the probability that she rolls a \(5\).
Find the probability that she rolls an even number.
Find the probability that she rolls a number greater than \(4\)
Find the probability that she rolls a number that is both: an even number and greater than \(4\).

SOLUTION

If we define the event:
- \(D\): rolling a 5
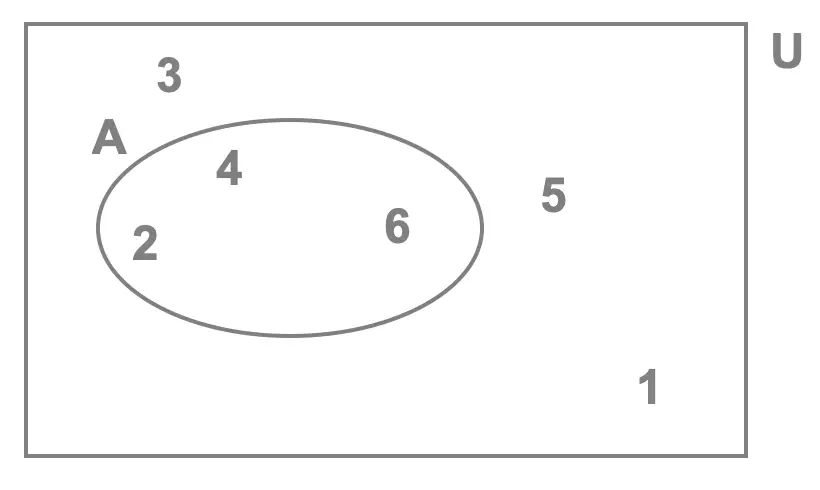then, since there is only one face of the die numbered \(5\), there is only one outcome corresponding to \(5\) and we can state: \[n\begin{pmatrix}D\end{pmatrix} = 1\] Using our formula we can then state \[\begin{aligned} p\begin{pmatrix}D\end{pmatrix} &= \frac{n\begin{pmatrix}D \end{pmatrix}}{n\begin{pmatrix}U\end{pmatrix}} \\ p\begin{pmatrix}D\end{pmatrix} & = \frac{1}{6} \end{aligned}\] The probability that Clara rolls a \(5\) is \(p\begin{pmatrix}D\end{pmatrix} = \frac{1}{6}\)

We start by defining the event:
- \(A\): rolling an even number.
Since there are three faces of the die with an even number, \(2\), \(4\) and \(6\), we can state: \[n\begin{pmatrix}A\end{pmatrix} = 3\] using our formula we can now state: \[\begin{aligned} p\begin{pmatrix}A \end{pmatrix} &= \frac{n\begin{pmatrix}A \end{pmatrix}}{n\begin{pmatrix}U\end{pmatrix}} \\ & = \frac{3}{6} \\ p\begin{pmatrix}A \end{pmatrix} &= \frac{1}{2} \end{aligned}\] The probability that Clara rolls an even number is \(p\begin{pmatrix}A\end{pmatrix} = \frac{1}{2}=0.5\).

We start by defining the event:
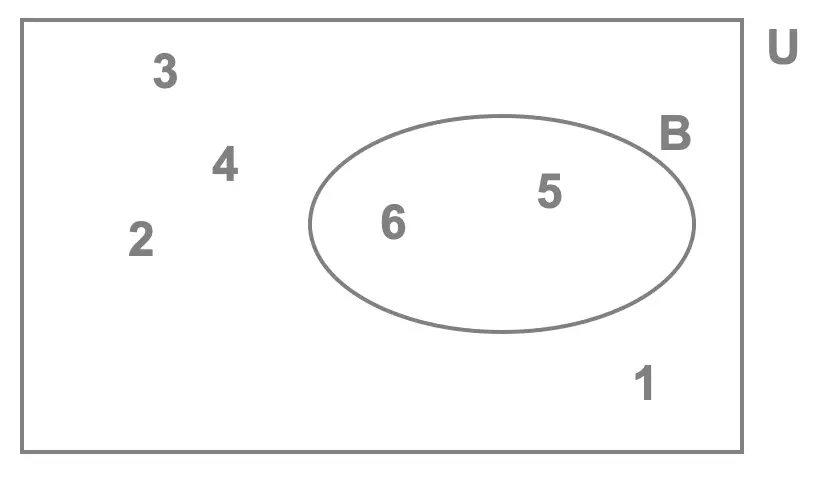
- \(B\): rolling a number greater than \(4\)
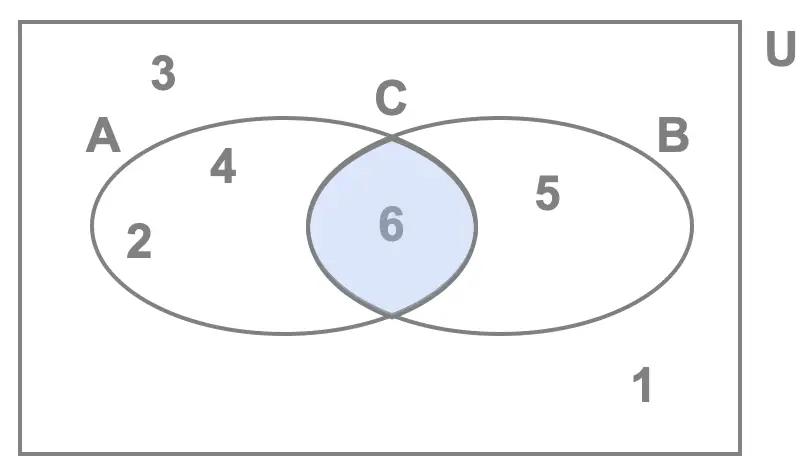There are two faces on the die with numbers greater than \(4\), those are \(5\) and \(6\), so we can write: \[n\begin{pmatrix} B \end{pmatrix} = 2\] Using our formula we can now state: \[\begin{aligned} p\begin{pmatrix} B \end{pmatrix} &= \frac{n\begin{pmatrix}B \end{pmatrix}}{n\begin{pmatrix}U \end{pmatrix}} \\ & = \frac{2}{6} \\ p\begin{pmatrix} B \end{pmatrix} & = \frac{1}{3} \end{aligned}\] The probability that Clara rolls a number greater than \(4\) is \(p\begin{pmatrix}B\end{pmatrix} = \frac{1}{3}\).

We start by defining the event:
- \(C\): rolling an even number greater than \(4\)
Only one outcome is both an even number and greater than \(4\), that's \(6\), so: \[n\begin{pmatrix} C \end{pmatrix} = 1\] Using our formula we can now state: \[\begin{aligned} p\begin{pmatrix} C \end{pmatrix} &= \frac{n\begin{pmatrix}C \end{pmatrix}}{n\begin{pmatrix}U \end{pmatrix}} \\ & = \frac{1}{6} \\ p\begin{pmatrix} C \end{pmatrix} & = \frac{1}{6} \end{aligned}\] The probability that Clara rolls an even number that is greater than \(4\) is \(p\begin{pmatrix}C\end{pmatrix} = \frac{1}{6}\). Note: event \(C\) corresponds to the outcome that is simultaneously (is both) an event \(A\) and an event \(B\). On the Venn diagram it corresponds to the area where the two sets overlap.