Probability of a Single Event
In this section we learn the formula for calculating the probability of a single event. In each of the examples we see here we'll use the terminology (experiment, outcomes, event, ... ) learnt in the previous section.
Formula for the Probability of a Single Event
Given an experiment and an event \(A\), the probability of event \(A\) occurring is given by: \[p\begin{pmatrix}A\end{pmatrix} = \frac{\text{number of outcomes corresponding to \(A\)}}{\text{total number of outcomes}}\] In this set of notes we'll be using the notation: \[p\begin{pmatrix}A\end{pmatrix} = \frac{n\begin{pmatrix}A\end{pmatrix}}{n\begin{pmatrix}U\end{pmatrix}}\] where:
- \(n\begin{pmatrix}A\end{pmatrix}\) is the number of outcomes corresponding to event \(A\)
- \(n\begin{pmatrix}U\end{pmatrix}\) is the total number of outcomes of the experiment.
Example 1
An unbiased die is rolled. What is the probability of obtaining a \(5\)?
Solution
When rolling an unbiased die, there are \(6\) possible outcomes:
We can define an event \(A\) as: \[A: \ \text{rolling a 5}\] Only one face of the die shows the number \(5\), so the number of ways event \(A\) can occur is \(1\), \(n\begin{pmatrix}A\end{pmatrix} = 1\). The probability of rolling a \(5\) is therefore: \[p\begin{pmatrix}A\end{pmatrix} = \frac{n\begin{pmatrix}A\end{pmatrix}}{n\begin{pmatrix}U\end{pmatrix}}\] That's: \[p\begin{pmatrix}A\end{pmatrix} = \frac{1}{6} \approx 17\%\] The probability of rolling a \(5\) is therefore \(p\begin{pmatrix}A\end{pmatrix} = \frac{1}{6}\), which is (approximately) a \(17\%\) chance.
Example 2
A whole number between \(1\) and \(20\) included is picked at random. What is the probability that the number picked is a prime number?
Solution
Since the number is picked amongst \(20\) whole numbers, the total number of possible outcomes is \(20\). So we can write \(n\begin{pmatrix}U\end{pmatrix} = 20\).
The prime numbers between \(1\) and \(20\), included, are:
2, 3, 5, 7, 11, 13, 17 and 19
Since there are \(8\) prime numbers between \(1\) and \(20\), the number of wauys event \(A\) can occur is: \(n\begin{pmatrix}A\end{pmatrix} = 8\) and we can calculate the probability: \[\begin{aligned} p\begin{pmatrix}A\end{pmatrix} & = \frac{n\begin{pmatrix}A\end{pmatrix}}{\begin{pmatrix}U\end{pmatrix}} \\ & = \frac{8}{20} \\ & = \frac{2}{5} \\ p\begin{pmatrix}A\end{pmatrix} & = 0.4 \end{aligned}\] The probability that the number be prime is \(p\begin{pmatrix}A\end{pmatrix} = 0.4\).
Example 3
- it stops on Blue
- it stops on Orange
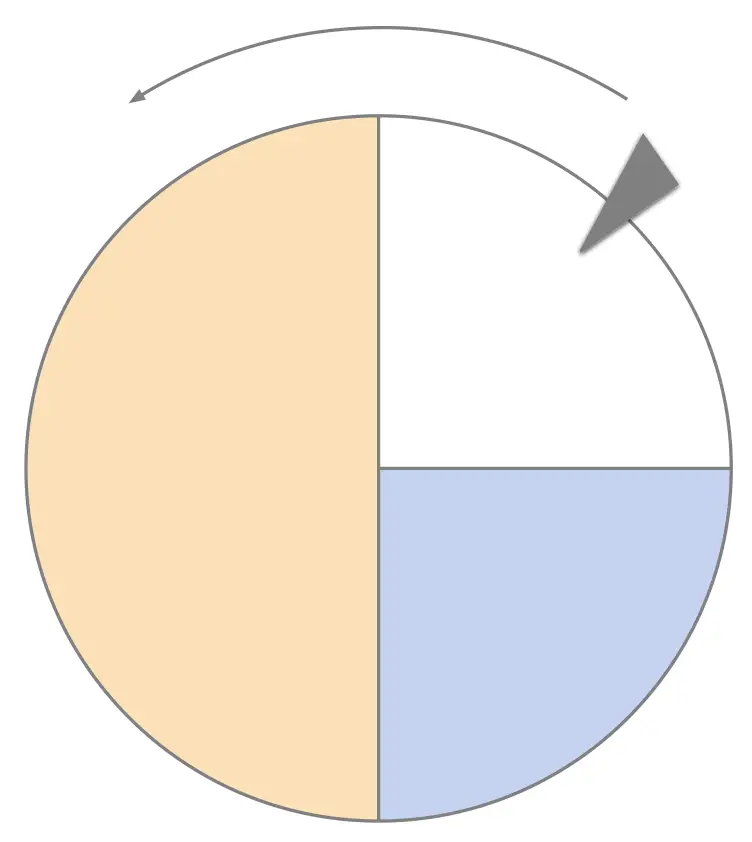
Solution
- 1 White region
- 1 Blue region
- 2 Orange regions
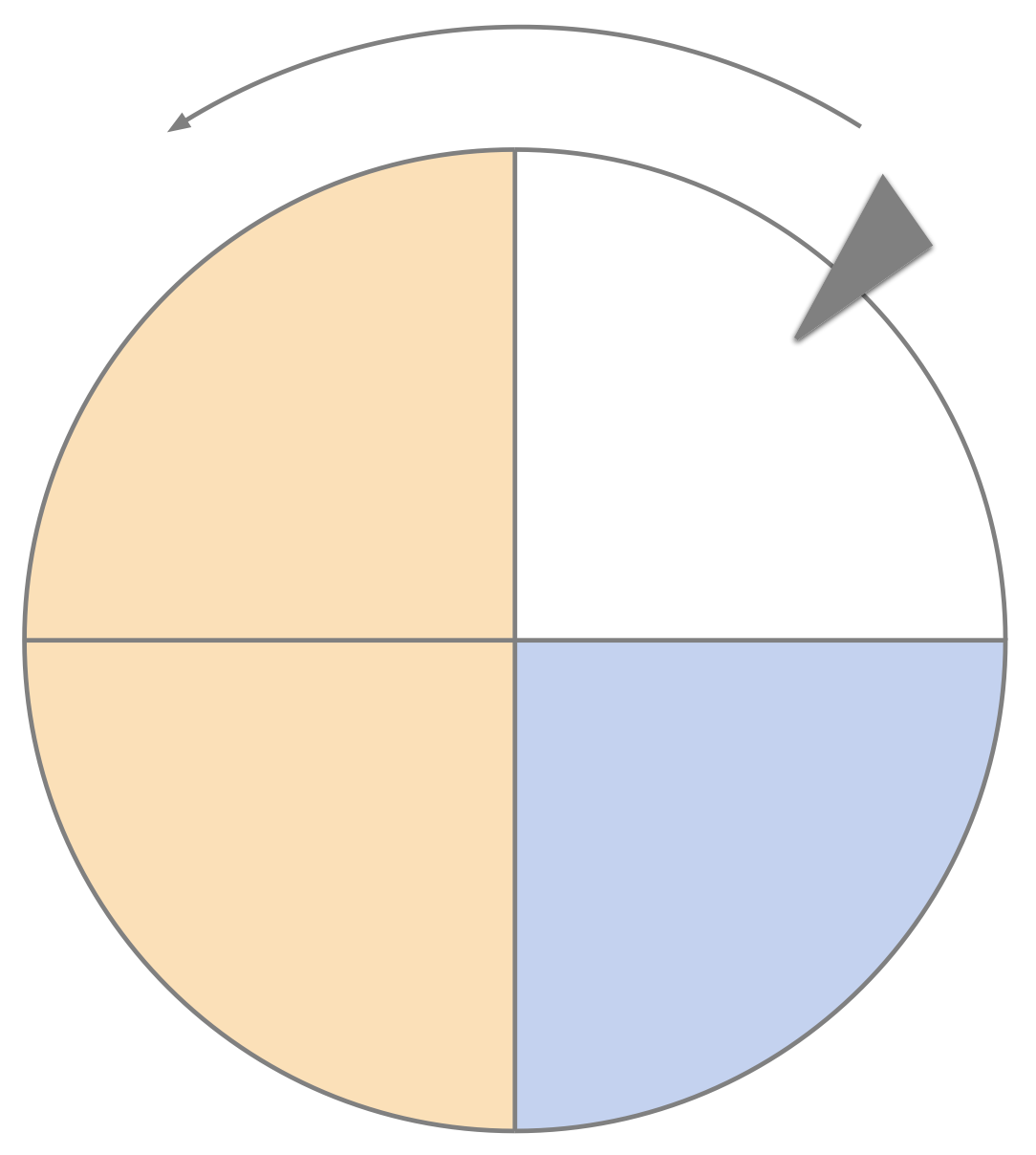
- We can define the event \(B\) as: \[B: \ \text{the spinner stops on Blue}\] Since there is "only" one Blue region the number of outcomes corresponding to Blue is \(n\begin{pmatrix}B\end{pmatrix}=1\). We can therefore state: \[\begin{aligned} p\begin{pmatrix}B\end{pmatrix} & = \frac{n\begin{pmatrix} B\end{pmatrix}}{n\begin{pmatrix}U\end{pmatrix}}\\ & = \frac{1}{4} \\ p\begin{pmatrix}B\end{pmatrix} & = 0.25 \end{aligned}\] The probability of the spinner sopping on blue is therefore \(p\begin{pmatrix}B\end{pmatrix} = 0.25\).
- We can define the event \(O\) as: \[O: \ \text{the spinner stops on Orange}\] Sincer there are 2 Orange regions (2 quarters) the number of outcomes corresponding to the event Orange, \(O\), is \(n\begin{pmatrix}O\end{pmatrix}=2\). So: \[\begin{aligned} p\begin{pmatrix}O\end{pmatrix} & = \frac{n\begin{pmatrix} O\end{pmatrix}}{n\begin{pmatrix}U\end{pmatrix}}\\ & = \frac{2}{4} \\ & = \frac{1}{2} \\ p\begin{pmatrix}O\end{pmatrix} & = 0.5 \end{aligned}\] The probability of the spinner sopping on orange is therefore \(p\begin{pmatrix}O\end{pmatrix} = 0.5\).
Scan this QR-Code with your phone/tablet and view this page on your preferred device.
Subscribe Now and view all of our playlists & tutorials.